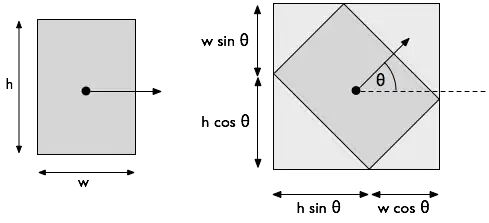
I don't know if this is the most efficient method, but I would just calculate the new positions of the vertices and based on that data find out the AABB. So for example,
Vertex v0, v1, v2, v3;
// in the local coordinates of the rectangle
// so for example v0 is always 0,0 and width and height define the others
// put some values to v0..v3
glLoadIdentity();
glTranslatef(the position of the rectangle);
glTranslatef(center_point);
glRotatef(angle, 0,0,1);
glTranslatef(-center_point);
GLfloat matrix[16];
glGetFloatv(GL_MODELVIEW_MATRIX, matrix);
v0 = multiply_matrix_by_vector(matrix, v0);
v1 = multiply_matrix_by_vector(matrix, v1);
v2 = multiply_matrix_by_vector(matrix, v2);
v3 = multiply_matrix_by_vector(matrix, v3);
AABB = find_the_minimums_and_maximums(v0, v1, v2, v3);
If you don't know how to multiply a matrix by vector, try googling it.
Also note that since the matrix dimensions are 4x4, the vectors for the vertices also need to be 4-dimensional. You can convert a 2D vector to a 4D vector by adding a third component 0 (zero) and a fourth component 1 (one). After the multiplication has been done, you can convert the resulting 4D vector back to 2D by dividing the x and y components by the fourth component and simply by ignoring the third component because you don't need a third dimension.
Since matrix multiplications might be a quite processor-heavy operation, this approach might be good only, if you don't need to update a lot of AABBs very often.