Untested pseudo-code because my lunch break is nearly over:
You have a multi-root tree, with one chosen principal root.
For each root, create a subgraph consisting of all reachable nodes for that root.
Starting with the principal root (root a), compute the distance/shortest path length to the root for all nodes in the corresponding subgraph A.
Find all subgraphs that share at least one node with the principal subgraph, and select the subgraph (subgraph B) that has the node (node x) with the smallest distance to the principal root.
Compute the distance to the root b for all nodes in subgraph B. Add the distance d(node x, root a). Subtract the distance d(node x, root b).
Create the union of subgraph A and B. Repeat steps 3-5 until no roots remain.
Subtract the maximum distance & reverse the sign such that principal root has the largest distance/order value.
Edit:
My pseudocode works (*). I blame user error. ;-)
#!/usr/bin/env python
"""
https://stackoverflow.com/q/66584661/
"""
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
def hierarchical_layout(graph):
longest_path = nx.algorithms.dag.dag_longest_path(graph)
principal_root = longest_path[0]
roots = [node for node, degree in list(graph.in_degree) if degree==0]
subgraphs = {root : create_subgraph(graph, root) for root in roots}
# Starting with the principal root (root a), compute the
# longest path length to the root for all nodes in the
# corresponding subgraph A.
node_to_level = single_source_longest_dag_path_length(subgraphs[principal_root], principal_root)
explored = subgraphs[principal_root]
del subgraphs[principal_root]
while len(explored) < len(graph):
# Find all subgraphs that share at least one node with the
# principal subgraph, and select the subgraph (subgraph B) that
# has the node (node x) with the smallest distance to the
# principal root.
minimum_cost = np.inf
minimum_cost_node = None
minimum_cost_root = None
for root, subgraph in subgraphs.items():
for node in subgraph.nodes:
if node in node_to_level:
if node_to_level[node] < minimum_cost:
minimum_cost = node_to_level[node]
minimum_cost_node = node
minimum_cost_root = root
assert minimum_cost_node, "Could not find a connected subgraph."
# Compute the distance to the root b for all nodes in subgraph
# B. Add the distance d(node x, root a). Subtract the distance
# d(node x, root b).
path_lengths = [len(path) for path in nx.all_simple_paths(subgraphs[minimum_cost_root], minimum_cost_root, minimum_cost_node)]
offset = np.max(path_lengths) - 1
for node, distance in single_source_longest_dag_path_length(subgraphs[minimum_cost_root], minimum_cost_root).items():
if not node in node_to_level:
node_to_level[node] = distance + minimum_cost - offset
# Create the union of subgraph A and B.
explored = nx.compose(explored, subgraphs[minimum_cost_root])
del subgraphs[minimum_cost_root]
return node_to_level
def create_subgraph(G, node):
# https://stackoverflow.com/a/45678930/2912349
nodes = nx.single_source_shortest_path(G,node).keys()
return G.subgraph(nodes)
def single_source_longest_dag_path_length(graph, s):
# from AlaskaJoslin's comment to https://stackoverflow.com/a/60978007/2912349
dist = dict.fromkeys(graph.nodes, -float('inf'))
dist[s] = 0
topo_order = nx.topological_sort(graph)
for n in topo_order:
for s in graph.successors(n):
if dist[s] < dist[n] + 1:
dist[s] = dist[n] + 1
return dist
if __name__ == '__main__':
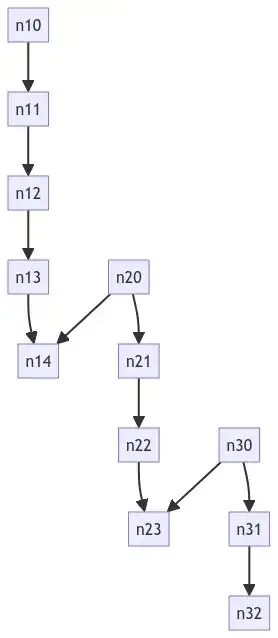
# edge_list = [
# ("n10", "n11"),
# ("n11", "n12"),
# ("n12", "n13"),
# ("n13", "n14"),
# ("n20", "n21"),
# ("n20", "n14"),
# ("n21", "n22"),
# ("n22", "n23"),
# ("n30", "n23"),
# ("n30", "n31"),
# ("n31", "n32"),
# ]
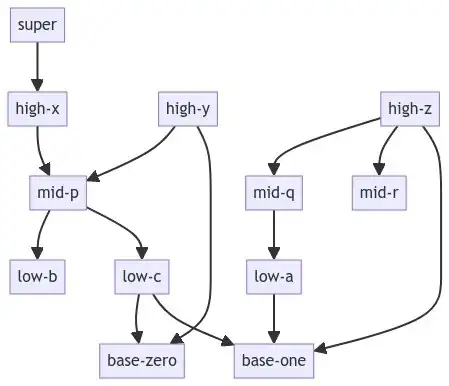
edge_list = [
("low-a", "base-one"),
("low-c", "base-zero"),
("low-c", "base-one"),
("mid-p", "low-b"),
("mid-p", "low-c"),
("mid-q", "low-a"),
("high-x", "mid-p"),
("high-y", "mid-p"),
("high-y", "base-zero"),
("high-z", "mid-q"),
("high-z", "mid-r"),
("high-z", "base-one"),
("super", "high-x"),
]
graph = nx.DiGraph()
graph.add_edges_from(edge_list)
node_to_level = hierarchical_layout(graph)
# reverse output format
distance_nodes_map = dict()
max_distance = np.max(list(node_to_level.values()))
for node, distance in node_to_level.items():
reversed_distance = max_distance - distance
if reversed_distance in distance_nodes_map:
distance_nodes_map[reversed_distance].add(node)
else:
distance_nodes_map[reversed_distance] = set([node])
# print(distance_nodes_map)
for ii, nodes in sorted(distance_nodes_map.items())[::-1]:
print(f"{ii} : {nodes}")
Yields:
# 4 : {'super'}
# 3 : {'high-x', 'high-y', 'high-z'}
# 2 : {'mid-p', 'mid-r', 'mid-q'}
# 1 : {'low-a', 'low-b', 'low-c'}
# 0 : {'base-one', 'base-zero'}
(*) "subtract distance d(node x, root b)" naturally implied the longest path length between node x and root b. Obviously.