import os
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
csv_path = os.path.join('', 'graph.csv')
graph = pd.read_csv(csv_path)
y = graph['y'].copy()
x = graph.drop('y', axis=1)
pipeline = Pipeline([('pf', PolynomialFeatures(2)), ('clf', LinearRegression())])
pipeline.fit(x, y)
predict = [[16], [20], [30]]
plt.plot(x, y, '.', color='blue')
plt.plot(x, pipeline.predict(x), '-', color='black')
plt.plot(predict, pipeline.predict(predict), 'o', color='red')
plt.show()
My graph.csv:
x,y
1,1
2,2
3,3
4,4
5,5
6,5.5
7,6
8,6.25
9,6.4
10,6.6
11,6.8
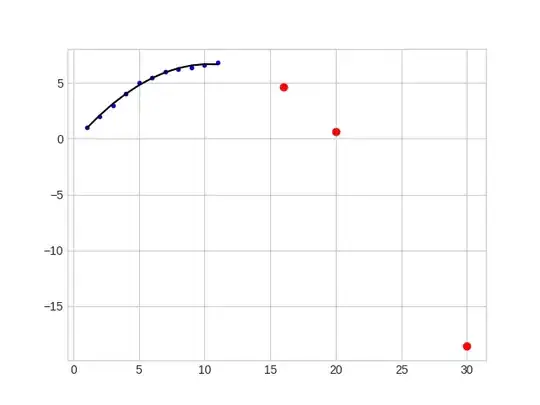
The result produced:
It clearly is producing wrong predictions; with each x, y should increase.
What am I missing? I tried changing degrees, but it doesn't get much better. When I use degree of 4 for example, y increases very very rapidly.