The problem
I implemented velocity verlet algorithm to compute trajectories of 2 bodies interacting with each other gravitationally (newtonian gravity only). Orbiting smaller body has a very small mass, body that is in the center of the orbit has a large mass.
In theory Velocity Verlet should not change total energy of the system (it will oscilate but over time the average will remain close to the initial energy).
However in practice I observed increase of energy over time.
Results
Here are some results which illustrate the problem. All simulations were performed with a timestep dt=0.001. Orbited body had a mass of 1000 and gravitational constant of the universe was set to G=1.0
In all cases smaller body initial position was {0, 0, 1} and it's initial velocity was {0, 32, 0}. Initial velocity of larger body was {0,0,0}.
Case 1 (small body mass = 0.00001)
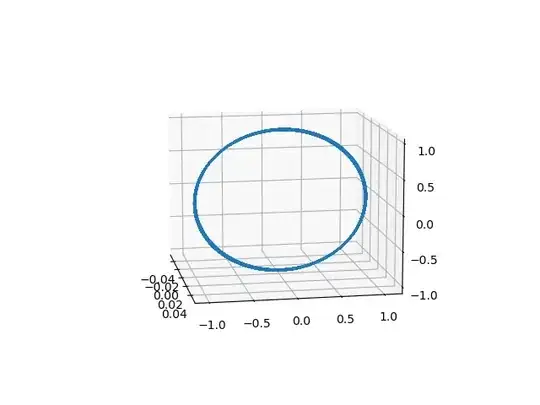
Here is the trajectory of the smaller body:
And here is energy over 100k steps.
As we can see the energy does not change by a lot. Small changes are likely due to inaccuracies in the calculations.
Case 1 (small body mass = 0.001)
Here is trajectory of the orbiting body:
And here is total energy:
As we can see now system is gaining energy.
Case 3 (small body mass = 1)
Here is trajectory of the orbiting body:
And here is total energy:
Now we are gaining a lot of energy.
code
Here is the source code that is performing all calculations:
Code for advancing integrator:
void Universe::simulation_step()
{
for(std::size_t i=0; i<get_size(); i++)
{
// Verlet step 1: Compute v(t + dt/2) = v(t) + 0.5*dt*a(t)
const Vector3D<Real> vel_half_step = {
velocity(i, 0) + static_cast<Real>(0.5)*sim_config.timestep*acceleration(i, 0),
velocity(i, 1) + static_cast<Real>(0.5)*sim_config.timestep*acceleration(i, 1),
velocity(i, 2) + static_cast<Real>(0.5)*sim_config.timestep*acceleration(i, 2)
};
// Verlet step 2: Compute x(t + dt) = x(t) + v(t + dt/2)*dt
position(i, 0) += vel_half_step.x*sim_config.timestep;
position(i, 1) += vel_half_step.y*sim_config.timestep;
position(i, 2) += vel_half_step.z*sim_config.timestep;
// Verlet step 3: update forces and update acceleration.
const Vector3D<Real> forces = compute_net_grawitational_force(i);
acceleration(i, 0) = forces.x/mass(i);
acceleration(i, 1) = forces.y/mass(i);
acceleration(i, 2) = forces.z/mass(i);
// Verlet step 4: update velocity to the full timestep.
velocity(i, 0) = vel_half_step.x + static_cast<Real>(0.5)*sim_config.timestep*acceleration(i, 0);
velocity(i, 1) = vel_half_step.y + static_cast<Real>(0.5)*sim_config.timestep*acceleration(i, 1);
velocity(i, 2) = vel_half_step.z + static_cast<Real>(0.5)*sim_config.timestep*acceleration(i, 2);
}
sim_time += sim_config.timestep;
}
Here is code for computing net gravitational force acting on the body:
Vector3D<Real> Universe::compute_net_grawitational_force(std::size_t i)
{
Vector3D<Real> accumulated_force = {0,0,0};
const Vector3D<Real> r2 = {
position(i, 0),
position(i, 1),
position(i, 2)
};
const Real m1 = mass(i);
for(std::size_t k=0; k<get_size(); k++)
{
if(k == i)
continue;
const Vector3D<Real> distace_vec = {
r2.x - position(k, 0),
r2.y - position(k, 1),
r2.z - position(k, 2),
};
const Real distance = distace_vec.norm2();
// Compute term that will be multipled by distance vector.
const Real a = (-1*sim_config.G*m1*mass(k))/
(distance*distance*distance);
// Compute and add new force acting on the body.
accumulated_force.x += distace_vec.x*a;
accumulated_force.y += distace_vec.y*a;
accumulated_force.z += distace_vec.z*a;
}
return accumulated_force;
}
Here is code that implements norm2():
template<typename T>
struct Vector3D
{
T x;
T y;
T z;
T norm2() const
{
return sqrt(x*x + y*y + z*z);
}
};
Finally here is code that computes results plotted previously:
std::vector<Real> x, y, z, energy;
x.resize(NSTEPS);
y.resize(NSTEPS);
z.resize(NSTEPS);
energy.resize(NSTEPS);
for(std::size_t i=0; i<NSTEPS; i++)
{
universe.simulation_step();
const Vector3D<Real> pos1 =
{
universe.get_positions()(0, 0),
universe.get_positions()(0, 1),
universe.get_positions()(0, 2)
};
const Vector3D<Real> pos2 =
{
universe.get_positions()(1, 0),
universe.get_positions()(1, 1),
universe.get_positions()(1, 2)
};
x[i] = pos2.x;
y[i] = pos2.y;
z[i] = pos2.z;
// Compute total kinetic energy of the system.
const Vector3D<Real> vel1 =
{
universe.get_velocities()(0, 0),
universe.get_velocities()(0, 1),
universe.get_velocities()(0, 2),
};
const Vector3D<Real> vel2 =
{
universe.get_velocities()(1, 0),
universe.get_velocities()(1, 1),
universe.get_velocities()(1, 2),
};
const Real mass1 = universe.get_masses()(0);
const Real mass2 = universe.get_masses()(1);
const Real spd1 = vel1.norm2();
const Real spd2 = vel2.norm2();
energy[i] = (spd1*spd1)*mass1*static_cast<float>(0.5);
energy[i] += (spd2*spd2)*mass2*static_cast<float>(0.5);
// Compute total potential energy
const Vector3D<Real> distance_vec =
{
pos1.x - pos2.x,
pos1.y - pos2.y,
pos1.z - pos2.z
};
const Real G = universe.get_sim_config().G;
energy[i] += -G*((mass1*mass2)/distance_vec.norm2());
}
Type Real is float.
My theories
I'm a beginner when it comes to numerical integration (that's why I posted this question here). However here are some theories about what might be wrong:
- There is some pitfall in the Velocity Verlet algorithm when it comes to n>=2 and I've fallen into it.
- There is implementation error somewhere in the above code and I don't see it.
- Errors due to floating point number calculations accumulate due to small movements of the large body. (Likely not the case see edit below.)
- During attempts to debug this I've come across
Energy driftin molecular dynamics simulation. Maybe this is what is happening here?
It doesn't seem like the orbit is falling apart but it is not the result that I expected and I want to know why.
Can someone help me solve this mystery?
Edit:
I have tested double precision and only change is that now the energy of the smallest orbiting mass is much more stable.
Now increasing trend can be seen even for the smallest mass. This hints that it is not a problem with precision of calculations.