Sliding window on an image to calculate variance of pixels in that window

Question

I am trying to build a function that uses sliding window over and image and calculates the variance of pixels in the window and returns a bounding box where there is the most variance observed.

I'm new to coding and I've tried solutions from this post but I don't know how to input image in that instead of array.

I'm on a deadline here and been trying this since a while so any help is much appreciated . TIA

Edit: Also, if someone could help me with how to call the rolling_window_lastaxis function and modify it to what I'm trying to do then it would mean a lot.

Answer 1

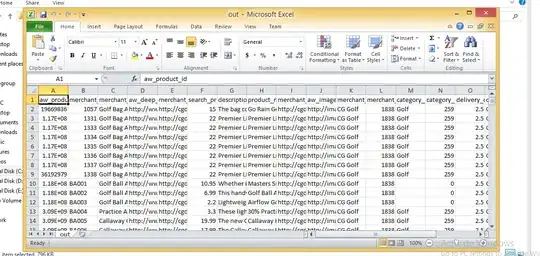
Here is one way to compute the sliding window variance (or standard deviation) using Python/OpenCV/Skimage.

This approach makes use of the following form for computing the variance (see https://en.wikipedia.org/wiki/Variance):

Variance = mean of square of image - square of mean of image

However, since the variance will be outside the 8-bit range, we take the square root to form the standard deviation.

I also use the (local) mean filter from the Skimage rank filter module.

Input:

import cv2
import numpy as np
from skimage.morphology import rectangle
import skimage.filters as filters

# Variance = mean of square of image - square of mean of image
# See # see https://en.wikipedia.org/wiki/Variance

# read the image
# convert to 16-bits grayscale since mean filter below is limited 
# to single channel 8 or 16-bits, not float
# and variance will be larger than 8-bit range
img = cv2.imread('lena.png', cv2.IMREAD_GRAYSCALE).astype(np.uint16)

# compute square of image
img_sq = cv2.multiply(img, img)

# compute local mean in 5x5 rectangular region of each image
# note: python will give warning about slower performance when processing 16-bit images
region = rectangle(5,5)
mean_img = filters.rank.mean(img, selem=region)
mean_img_sq = filters.rank.mean(img_sq, selem=region)

# compute square of local mean of img
sq_mean_img = cv2.multiply(mean_img, mean_img)

# compute variance using float versions of images
var = cv2.add(mean_img_sq.astype(np.float32), -sq_mean_img.astype(np.float32))

# compute standard deviation and convert to 8-bit format
std = cv2.sqrt(var).clip(0,255).astype(np.uint8)

# save results
# multiply by 2 to make brighter as an example
cv2.imwrite('lena_std.png',2*std)

# show results
# multiply by 2 to make brighter as an example
cv2.imshow('std', 2*std)  
cv2.waitKey(0)
cv2.destroyAllWindows()

Local Standard Deviation Image for 5x5 Sliding Window:

ADDITION

Here is a version that finds the bounding box for the maximum average variance for the bounding box size and draws it on the variance image (actually standard deviation).

import cv2
import numpy as np
from skimage.morphology import rectangle
import skimage.filters as filters

# Variance = mean of square of image - square of mean of image
# See # see https://en.wikipedia.org/wiki/Variance

# set the bounding box size
bbox_size = 25

# read the image
# convert to 16-bits grayscale since mean filter below is limited 
# to single channel 8 or 16-bits, not float
# and variance will be larger than 8-bit range
img = cv2.imread('lena.png', cv2.IMREAD_GRAYSCALE).astype(np.uint16)

# compute square of image
img_sq = cv2.multiply(img, img)

# compute local mean in bbox_size x bbox_size rectangular region of each image
# note: python will give warning about slower performance when processing 16-bit images
region = rectangle(bbox_size, bbox_size)
mean_img = filters.rank.mean(img, selem=region)
mean_img_sq = filters.rank.mean(img_sq, selem=region)

# compute square of local mean of img
sq_mean_img = cv2.multiply(mean_img, mean_img)

# compute variance using float versions of images
var = cv2.add(mean_img_sq.astype(np.float32), -sq_mean_img.astype(np.float32))

# compute standard deviation and convert to 8-bit format
std = cv2.sqrt(var).clip(0,255).astype(np.uint8)

# find bbox_size x bbox_size region with largest var (or std)
# get the moving window average at each pixel
std_ave = (cv2.sqrt(var)).astype(np.uint8)

# find the pixel x,y with the largest mean
min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(std_ave)
x,y = max_loc
print("x:", x, "y:", y, "max:", max_val)

# draw rectangle for bounding box on copy of std image
result = std.copy()
result = cv2.merge([result, result, result])
cv2.rectangle(result, (x, y), (x+bbox_size, y+bbox_size), (0,0,255), 1)

# save results
# multiply by 2 to make brighter as an example
cv2.imwrite('lena_std.png',std)
cv2.imwrite('lena_std_bbox.png',result)

# show results
# multiply by 2 to make brighter as an example
cv2.imshow('std', std)  
cv2.imshow('result', result)  
cv2.waitKey(0)
cv2.destroyAllWindows()

x: 208 y: 67 max: 79.0

Resulting Bounding Box:

Answer 2

An alternative method to compute the windowed/rolling variance in regions of WxH is to use just numpy and scipy with convolutions, which are computed fairly quickly. An example:

import numpy as np
import scipy.signal
# Create image data
original = np.zeros((811,123))
img = original + np.random.normal(0, 1, original.shape)
# Create averaging kernel
H, W = 5, 5
mean_op = np.ones((H,W))/(H*W)
# Carry out convolution to compute mean of square, and square of mean
mean_of_sq = scipy.signal.convolve2d( img**2, mean_op, mode='same', boundary='symm')
sq_of_mean = scipy.signal.convolve2d( img   , mean_op, mode='same', boundary='symm') **2
win_var    = mean_of_sq - sq_of_mean