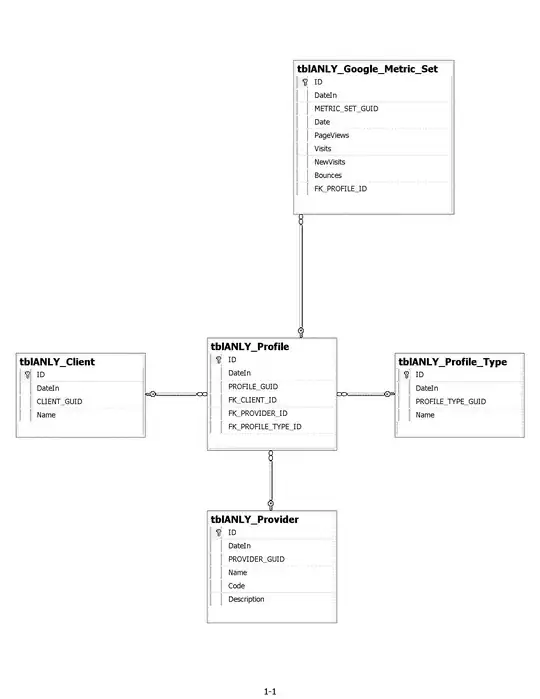
I wish to create a continuous probability distribution from this dataset.
The 'Value' shows a measured value and the 'Weight' is the probability of measuring this value in this measurement.
I already graphed the data. On the x-axis it shows the value, and the Y-axis the probability. But I wish to create an exact distribution to fit this data.
In my data-analysis I eventually wish to compare several data distributions by their parameters. I hope you guys can help me out.
| Line # | Value | Weight |
|---|---|---|
| 0 | 0.0538502 | 0.016508 |
| 1 | 0.0184823 | 0.0298487 |
| 2 | 0.0647929 | 0.0122637 |
| 3 | 0.0262852 | 0.0234716 |
| 4 | 0.0447611 | 0.0197072 |
| 5 | 0.0643164 | 0.0165399 |
| 6 | 0.0709176 | 0.0143751 |
| 7 | 0.0871276 | 0.012253 |
| 8 | 0.0341064 | 0.0197392 |
| 9 | 0.0593696 | 0.0143858 |
| 10 | 0.0436119 | 0.0202617 |
| 11 | 0.0505131 | 0.0191846 |
| 12 | 0.0378706 | 0.0207842 |
| 13 | 0.0298233 | 0.0250712 |
| 14 | 0.157727 | 0.0111866 |
| 15 | 0.0556603 | 0.0186408 |
| 16 | 0.0542849 | 0.017617 |
| 17 | 0.0395772 | 0.0180969 |
| 18 | 0.0694962 | 0.0117305 |
| 19 | 0.0343318 | 0.0229277 |
| 20 | 0.139291 | 0.00907511 |
| 22 | 0.0232517 | 0.0186514 |
| 23 | 0.207768 | 0.0069423 |
| 24 | 0.0156452 | 0.021872 |
| 25 | 0.117749 | 0.0100989 |
| 26 | 0.124017 | 0.0111973 |
| 27 | 0.0679313 | 0.0133407 |
| 28 | 0.0733413 | 0.0117198 |
| 29 | 0.100553 | 0.0133407 |
| 30 | 0.0695865 | 0.016508 |
| 31 | 0.117732 | 0.0138633 |
| 32 | 0.0540577 | 0.0170518 |
| 33 | 0.0736274 | 0.0170625 |
| 34 | 0.0332381 | 0.0293155 |
| 35 | 0.0803423 | 0.0159961 |
| 36 | 0.0465 | 0.0191846 |
| 37 | 0.0889299 | 0.0159854 |
| 38 | 0.053232 | 0.020251 |
| 39 | 0.131361 | 0.0122637 |
| 40 | 0.0233194 | 0.0240048 |
| 41 | 0.830735 | 0.0053107 |
| 42 | 0.341012 | 0.0069423 |
| 43 | 0.101263 | 0.0106534 |
| 44 | 0.127061 | 0.00959765 |
| 45 | 0.13706 | 0.0122637 |
| 46 | 0.120035 | 0.0106641 |
| 47 | 0.0801194 | 0.0138526 |
| 48 | 0.0617996 | 0.0165186 |
| 49 | 0.197555 | 0.0117305 |
| 50 | 0.0810635 | 0.0133301 |
| 51 | 0.0178539 | 0.0335811 |
| 52 | 0.0391433 | 0.0170518 |
| 53 | 0.0663863 | 0.0133194 |
| 54 | 0.0617675 | 0.0170625 |
| 55 | 0.00684359 | 0.0346582 |
| 56 | 0.0642299 | 0.0133301 |
| 57 | 0.00970105 | 0.0239941 |
| 58 | 0.0307687 | 0.0213068 |
| 59 | 0.0160796 | 0.0255937 |
| 60 | 0.0147901 | 0.0266388 |
| 61 | 0.073745 | 0.0122637 |
| 62 | 0.0420728 | 0.0207949 |
| 63 | 0.0211625 | 0.0207949 |
| 66 | 0.0241562 | 0.0255937 |
| 67 | 0.0329688 | 0.0239834 |
| 68 | 0.0739628 | 0.0181289 |
| 69 | 0.0149927 | 0.0266388 |
| 70 | 0.0130271 | 0.0378467 |
| 73 | 0.0107957 | 0.0351914 |
| 74 | 0.040447 | 0.0175744 |
| 75 | 0.00123215 | 0.0559756 |
| 76 | 0.0134575 | 0.0309151 |
| 77 | 0.00592594 | 0.0453116 |