Fit of multiple nonlinear curves with Python

Question

Let's say that we have a curve that have an n-number of curves that are contributing to its shape. In my basic example, working with NMR peaks, I have 3 peaks defined:

Here, I have used the following method for fitting these three peaks at once:

def lor_3(x, R1, F1, R2, F2, R3, F3):
return (R1) / (R1**2 + 4 * np.pi**2 * (x-F1)**2) +\
    (R2) / (R2**2 + 4 * np.pi**2 * (x-F2)**2) +\
    (R3) / (R3**2 + 4 * np.pi**2 * (x-F3)**2)

popt, pcov = optimize.curve_fit(lor_3, X, y, p0=[11, 750, 5.5, 800, 11, 850])

Code which works nicely to fit these kind of peaks. However, if I have a more complex case:

Then the situations is not that easy. I would have to define a lot of functions with 1, 2, 3, 6 or whatever peaks contributing to the total curve depending on the case.

Is there any optimal way to perform fit of N - curves with scipy.optimize.curve_fit or with other Python tool?

Thanks!

What is optimal in your opinion? The more curves you use, the smaller your error. It is a trade-off between model simplicity and minimizing the error. — joostblack, Apr 30 '21 at 07:24
Maybe something like this answer https://stackoverflow.com/questions/14189937/separate-mixture-of-gaussians-in-python ? — Stefan, Apr 30 '21 at 07:27

Max Pierini · Answer 1 · 2021-04-30T20:40:53.497

You can use lmfit (see https://lmfit.github.io/lmfit-py/examples/example_expression_model.html).

First, let's define a lor function (based on yours)

import numpy as np

def lor(x, R, F):
    y = R / (R**2 + 4 * np.pi**2 * (x-F)**2)
    return y

and some sample data

import matplotlib.pyplot as plt

x = np.linspace(0, 1000, 1000)

Rs =  np.array([7, 8,  11,  11,  7.5,  10, 5, 6, 3])
Fs = np.array([20, 210, 230, 250, 270, 300, 790, 800, 810])

Ys = lor(x, Rs.reshape(-1, 1), Fs.reshape(-1, 1))

for _y in Ys:
    plt.plot(x, _y)

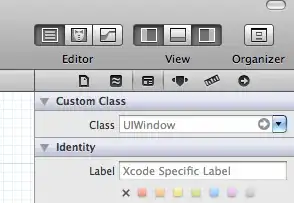
Now let's sum up all lor curves

y = Ys.sum(axis=0)

plt.plot(x, y)

Let's suppose this is the curve you actually want to fit.

To fit this curve, we can first find the peaks

from scipy.signal import find_peaks

peaks_idx = find_peaks(y)

peaks_x = x[peaks_idx[0]]
peaks_y = y[peaks_idx[0]]
peaks_x

array([ 20.02002002, 210.21021021, 230.23023023, 250.25025025,
       270.27027027, 300.3003003 , 789.78978979, 799.7997998 ,
       809.80980981])

and you see that are the Fs of our distinct lor functions

plt.plot(x, y)
plt.plot(peaks_x, peaks_y, 'r.')

Finally, we import ExpressionModel from lmfit and define a model string based on lor function and found peaks

from lmfit.models import ExpressionModel

_mod = []
for i, p in enumerate(peaks_x):
    _mod.append(f'R{i} / (R{i}**2 + 4 * pi**2 * (x-{p})**2)')
model = ' + '.join(_mod)
model

'R0 / (R0**2 + 4 * pi**2 * (x-20.02002002002002)**2) + R1 / (R1**2 + 4 * pi**2 * (x-210.21021021021022)**2) + R2 / (R2**2 + 4 * pi**2 * (x-230.23023023023026)**2) + R3 / (R3**2 + 4 * pi**2 * (x-250.25025025025028)**2) + R4 / (R4**2 + 4 * pi**2 * (x-270.2702702702703)**2) + R5 / (R5**2 + 4 * pi**2 * (x-300.3003003003003)**2) + R6 / (R6**2 + 4 * pi**2 * (x-789.7897897897899)**2) + R7 / (R7**2 + 4 * pi**2 * (x-799.7997997997999)**2) + R8 / (R8**2 + 4 * pi**2 * (x-809.8098098098098)**2)'

we can now initialize the model and parameters, that will be only Rs (because we already have Fs, the peaks)

mod = ExpressionModel(model)

params = mod.make_params()
# set initial value of params to 1
for p in params.items():
    mod.set_param_hint(p[0], value=1)

params = mod.make_params()

and fit the curve (where y is the curve you want to fit, i.e. the curve you got)

result = mod.fit(y, x=x)

Inspect results report

print(result.fit_report())

[[Model]]
    Model(_eval)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 81
    # data points      = 1000
    # variables        = 9
    chi-square         = 0.00426669
    reduced chi-square = 4.3054e-06
    Akaike info crit   = -12346.6724
    Bayesian info crit = -12302.5026
[[Variables]]
    R0:  7.00213482 +/- 0.09828903 (1.40%) (init = 1)
    R1:  8.19392889 +/- 0.13088578 (1.60%) (init = 1)
    R2:  11.1504879 +/- 0.21714760 (1.95%) (init = 1)
    R3:  11.1762542 +/- 0.21792883 (1.95%) (init = 1)
    R4:  7.84104148 +/- 0.12104425 (1.54%) (init = 1)
    R5:  10.2784143 +/- 0.19103875 (1.86%) (init = 1)
    R6:  5.34471739 +/- 0.05795283 (1.08%) (init = 1)
    R7:  6.25447147 +/- 0.07912175 (1.27%) (init = 1)
    R8:  3.46872840 +/- 0.02446415 (0.71%) (init = 1)

and check the plot

fig, ax = plt.subplots(figsize=(10, 5))
plt.plot(x, y, 'b', lw=1, label='observed')
plt.plot(x, result.best_fit, 'r-', label='best fit', ls='--')
plt.legend(loc='best')
plt.show()

Fit of multiple nonlinear curves with Python

1 Answers1