Here is a way that is sometimes faster than your "fast()" version, but only in a limited range of n (roughly between 30 and 1000) for a n x n array. The loop (fast()) is very hard to beat on large arrays, even using numba, and actually converges asymptotically to the time of simply a.sum(axis=0), which indicates that this is about as efficient as it gets for large arrays (kudos to your loop!)
The method, which I'll call sum_antidiagonals(), uses np.add.reduce() on a striped version of a and on a made-up mask from a relatively small 1D array that is striped to create the illusion of a 2D array (without consuming more memory).
Additionally, it is not limited to square arrays (but fast() can be easily adapted for this generalization as well, see fast_g() at the bottom of this post).
def sum_antidiagonals(a):
assert a.flags.c_contiguous
r, c = a.shape
s0, s1 = a.strides
z = np.lib.stride_tricks.as_strided(
a, shape=(r, c+r-1), strides=(s0 - s1, s1), writeable=False)
# mask
kern = np.r_[np.repeat(False, r-1), np.repeat(True, c), np.repeat(False, r-1)]
mask = np.fliplr(np.lib.stride_tricks.as_strided(
kern, shape=(r, c+r-1), strides=(1, 1), writeable=False))
return np.add.reduce(z, where=mask)
Notice that it isn't limited to a square array:
>>> sum_antidiagonals(np.arange(15).reshape(5,3))
array([ 0, 4, 12, 21, 30, 24, 14])
Explanation
To understand how that works, let's examine these striped arrays with an example.
Given an initial array a that is (3, 2):
a = np.arange(6).reshape(3, 2)
>>> a
array([[0, 1],
[2, 3],
[4, 5]])
# after calculating z in the function
>>> z
array([[0, 1, 2, 3],
[1, 2, 3, 4],
[2, 3, 4, 5]])
You can see that it is almost what we want to sum(axis=0), except that the lower and upper triangles are unwanted. What we would really like to sum looks like:
array([[0, 1, -, -],
[-, 2, 3, -],
[-, -, 4, 5]])
Enter the mask, which we can build starting from a 1D kernel:
kern = np.r_[np.repeat(False, r-1), np.repeat(True, c), np.repeat(False, r-1)]
>>> kern
array([False, False, True, True, False, False])
We use a funny slice: (1, 1), which means that we repeat the same row, but sliding by one element each time:
>>> np.lib.stride_tricks.as_strided(
... kern, shape=(r, c+r-1), strides=(1, 1), writeable=False)
array([[False, False, True, True],
[False, True, True, False],
[ True, True, False, False]])
We then just flip this left/right, and use it as the where argument for np.add.reduce().
Speed
b = np.random.normal(size=(1000, 1000))
# check equivalence with the OP's fast() function:
>>> np.allclose(fast(b), sum_antidiagonals(b))
True
%timeit sum_antidiagonals(b)
# 1.83 ms ± 840 ns per loop (mean ± std. dev. of 7 runs, 1000 loops each)
%timeit fast(b)
# 2.07 ms ± 15.2 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
In this case, it is a little bit faster, but only by about 10%.
On a 300x300 array, sum_antidiagonals() is 2.27x faster than fast().
However!
Even though putting together z and mask is very fast (the whole setup before np.add.reduce() takes only 46 µs in the 1000x1000 example above), the summation itself is O[r (r+c)], even though only O[r c] actual additions (where mask == True) are needed. There is therefore about 2x more operations done for a square array.
On a 10K x 10K array, this catches up with us:
fast takes 95ms, whereassum_antidiagonals takes 208 ms.
Comparison through range of sizes
We'll use the lovely perfplot package to compare speeds of a number of approaches through ranges of n:
perfplot.show(
setup=lambda n: np.random.normal(size=(n, n)),
kernels=[just_sum_0, fast, fast_g, nb_fast_i, nb_fast_ij, sum_antidiagonals],
n_range=[2 ** k for k in range(3, 16)],
equality_check=None, # because of just_sum_0
xlabel='n',
relative_to=1,
)
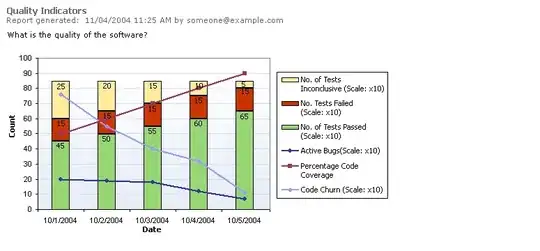
Observations
- As you can see,
sum_antidiagonals() speed advantage over fast() is limited to a range of n roughly between 30 and 1000.
- It never beats the
numba versions.
just_sum_0(), which is simply the summation along axis=0 (and thus a good bottom-line benchmark, almost impossible to beat), is only marginally faster for large arrays. That fact indicates that fast() is about as fast as it will get for large arrays.- Surprisingly,
numba detracts after a certain size (and that is after a first few runs to "burn in" the LLVM compilation). I am not sure why that is the case, but it seems to become significant for large arrays.
Full code for the other functions
(Including a simple generalization of fast to non-square arrays)
from numba import njit
@njit
def nb_fast_ij(a):
# numba loves loops...
r, c = a.shape
z = np.zeros(c + r - 1, dtype=a.dtype)
for i in range(r):
for j in range(c):
z[i+j] += a[i, j]
return z
@njit
def nb_fast_i(a):
r, c = a.shape
z = np.zeros(c + r - 1, dtype=a.dtype)
for i in range(r):
z[i:i+c] += a[i, :]
return z
def fast_g(a):
# generalizes fast() to non-square arrays, also returns the same dtype
r, c = a.shape
z = np.zeros(c + r - 1, dtype=a.dtype)
for i in range(r):
z[i:i+c] += a[i]
return z
def fast(A):
# the OP's code
n = A.shape[0]
retval = np.zeros(2*n-1)
for i in range(n):
retval[i:(i+n)] += A[i, :]
return retval
def just_sum_0(a):
# for benchmarking comparison
return a.sum(axis=0)