Simulate a two-dimensional random walk in a grid in R and plot with ggplot

Question

I was looking for a simple code that could simulate a two-dimensional random walk in a grid (using R), and then plot the data using ggplot.

In particular, I was interested to a random walk from few position (5 points) in a 2D grid to the center of the square grid. It is just for visualisation purposes.

And my idea was then to plot the results with ggplot on a discrete grid (as the one simulated), may be using the function geom_tile.

Do you have any suggestion for a pre-existing code that I could easily manipulate?

Answer 1

Here is a small example with a for loop. From here, you can simply adjust how X_t and Y_t are defined:

Xt = 0; Yt = 0
for (i in 2:1000)
{
  Xt[i] = Xt[i-1] + rnorm(1,0,1)
  Yt[i] = Yt[i-1] + rnorm(1,0,1)
}
df <- data.frame(x = Xt, y = Yt)
ggplot(df, aes(x=x, y=y)) + geom_path() + theme_classic() + coord_fixed(1)

Answer 2

EDIT ----

After chatting with OP I've revised the code to include a step probability. This may result in the walk being stationary much more frequently. In higher dimensions, you will need to scale your prob factor lower in order to compensate for more options.

finally, my function does not account for an absolute distance, it only considers points on the grid that are within a certain step size in all dimensions. For example, hypothetically, at position c(0,0) you could go to c(1,1) with this function. But I guess this is relative to the grid's connectiveness.

If the OP wants to only consider nodes that are within 1 (by distance) of the current position, then use the following version of move_step()

move_step <- function(cur_pos, grid, prob = 0.04, size = 1){
  opts <- grid %>%
    rowwise() %>%
    mutate(across(.fns = ~(.x-.env$cur_pos[[cur_column()]])^2,
                  .names = '{.col}_square_diff')) %>%
    filter(sqrt(sum(c_across(ends_with("_square_diff"))))<=.env$size) %>%
    select(-ends_with("_square_diff")) %>%
    left_join(y = mutate(cur_pos, current = TRUE), by = names(grid)) 
  new_pos <- opts %>%
    mutate(weight = case_when(current ~ 1-(prob*(n()-1)), #calculate chance to move, 
                              TRUE ~ prob),               #in higher dimensions, we may have more places to move
           weight = if_else(weight<0, 0, weight)) %>%    #thus depending on prob, we may always move.
    sample_n(size = 1, weight = weight) %>%
    select(-weight, -current)
  new_pos
}

library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(ggplot2)
library(gganimate)

move_step <- function(cur_pos, grid, prob = 0.04, size = 1){
  opts <- grid %>%
    filter(across(.fns =  ~ between(.x, .env$cur_pos[[cur_column()]]-.env$size, .env$cur_pos[[cur_column()]]+.env$size))) %>%
    left_join(y = mutate(cur_pos, current = TRUE), by = names(grid)) 
  new_pos <- opts %>%
    mutate(weight = case_when(current ~ 1-(prob*(n()-1)), #calculate chance to move, 
                              TRUE ~ prob),               #in higher dimensions, we may have more places to move
           weight = if_else(weight<0, 0, weight)) %>%    #thus depending on prob, we may always move.
    sample_n(size = 1, weight = weight) %>%
    select(-weight, -current)
  new_pos
}

sim_walk <- function(cur_pos, grid, grid_prob = 0.04, steps = 50, size = 1){
  iterations <- cur_pos
  for(i in seq_len(steps)){
    cur_pos <- move_step(cur_pos, grid, prob = grid_prob, size = size)
    iterations <- bind_rows(iterations, cur_pos)
  }
  iterations$i <- 1:nrow(iterations)
  iterations
}

origin <- data.frame(x = 0, y =0)
small_grid <- expand.grid(x = -1:1, y = -1:1)
small_walk <- sim_walk(cur_pos = origin,
                       grid = small_grid)

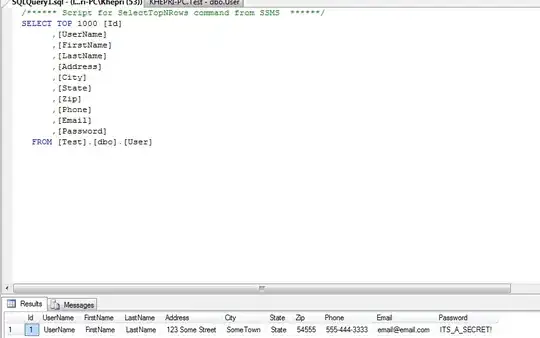
ggplot(small_walk, aes(x, y)) +
  geom_path() +
  geom_point(color = "red") +
  transition_reveal(i) +
  labs(title = "Step {frame_along}") +
  coord_fixed()

large_grid <- expand.grid(x = -10:10, y = -10:10)
large_walk <- sim_walk(cur_pos = origin,
                       grid = large_grid,
                       steps = 100)

ggplot(large_walk, aes(x,y)) +
  geom_path() +
  geom_point(color = "red") +
  transition_reveal(i)  +
  labs(title = "Step {frame_along}") +
  xlim(c(-10,10)) + ylim(c(-10,10))+
  coord_fixed()

large_walk %>% 
  count(x, y) %>%
  right_join(y = expand.grid(x = -10:10, y = -10:10), by = c("x","y")) %>%
  mutate(n = if_else(is.na(n), 0L, n)) %>%
  ggplot(aes(x,y)) +
  geom_tile(aes(fill = n)) +
  coord_fixed()

multi_dim_walk <- sim_walk(cur_pos = data.frame(x = 0, y = 0, z = 0),
                           grid =  expand.grid(x = -20:20, y = -20:20, z = -20:20),
                           steps = 100, size = 2)

library(cowplot)
plot_grid(
  ggplot(multi_dim_walk, aes(x, y)) + geom_path(),
  ggplot(multi_dim_walk, aes(x, z)) + geom_path(),
  ggplot(multi_dim_walk, aes(y, z)) + geom_path())

^{Created on 2021-05-06 by the reprex package (v1.0.0)}

Answer 3

Here is a base R option using Reduce + replicate + plot for 2D random walk process

set.seed(0)
plot(
  setNames(
    data.frame(replicate(
      2,
      Reduce(`+`, rnorm(99), init = 0, accumulate = TRUE)
    )),
    c("X", "Y")
  ),
  type = "o"
)