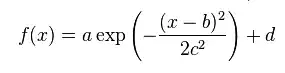Suppose we want to do a simple 'descriptive model of income.' Suppose we have three groups, North, Central, and South (think US regions). Comparing otherwise similar groups, suppose average income in the North is 130, Central is 80, and South is 60. Suppose equal group sizes, so mean is 90.
There should be a way, in a (linear regression) model, to report coefficients as differences from overall means (in a multivariate context, ‘all else equal’) and get one for each:
$\beta_{North} = 40$
$\beta_{Central} = -10$
$\beta_{South} = -30$
And skip the intercept, obviously.
This seems most intuitive to me. But I can’t for the life of me figure out how to get this with R’s ‘contrast coding’. (And also, that seems to mess up the variable names).
Set parameters for my simulation/mwe
m_inc <- 90
b_n <- 40
b_c <- -10
b_s <- -30
sd_prop <- 0.5 #sd as share of mean
pop_per <- 1000
Simulated data
set.seed(100)
n_income <- rnorm(pop_per, m_inc + b_n, (m_inc + b_n)*sd_prop)
c_income <- rnorm(pop_per, m_inc + b_c, (m_inc + b_s)*sd_prop)
s_income <- rnorm(pop_per, m_inc + b_s, (m_inc + b_s)*sd_prop)
noise_var <- rnorm(pop_per*3, 0, (m_inc + b_s)*sd_prop)
i_df <- tibble(
region = rep( c("n", "c", "s"), c(pop_per, pop_per, pop_per) ),
income = c(n_income, c_income, s_income),
noise_var
) %>%
mutate(region = as.factor(region))
i_df %>% # Summary by group using purrr
split(.$region) %>%
purrr::map(summary)
Looks close enough.
Now I want to 'model income' to examine the differences by region 'controlling for other factors'. To illustrate the issue, let's make the south the base group. I set the default contr.treatment in case you have reset it.
i_df <- i_df %>% mutate(region = relevel(region, ref="s"))
options(contrasts = rep ("contr.treatment", 2))
(
basic_lm <- i_df %>% lm(income ~ region + noise_var, .)
)
The standard thing: intercept is (approximately) the mean for the 'base group', the south, and the coefficients regionc and regionn represent the relative adjustments for these, roughly +20 and +70.
This is standard 'dummy coding', i.e., 'treatment coding', the default i R.
We can adjust this default (for unordered variables) to something called 'sum contrast coding' for both unordered and ordered
options(contrasts = rep ("contr.sum", 2))
(
basic_lm_cc <- i_df %>% lm(income ~ region + noise_var, .)
)
Now this seems to get us the adjustment coefficients we are looking for, but
- The names of the regions are lost; how do I know which is which?
- It is apparently reporting the adjustment coefficients for s (south) and c (central). Not very intuitive.
This seems to be the case no matter how we relevel the region to set a particular base group (I tried it) ... the coefficients don't change.
I found a solution, but it's not the "right way". I de-mean the outcome (income) variable, and force a 0 intercept:
i_df %>%
mutate(m_inc = mean(income)) %>%
lm(income - m_inc ~ 0 + region + noise_var, .)
Yay! This is what I wanted, and miraculously the variable names are preserved. But it seems a weird way to do it. Also note that, with the above code, this set of coefficients appears no matter which contrast matrix I force, whether sum or treatment.
How can this be done the 'right way' with contrast coding or another tool?