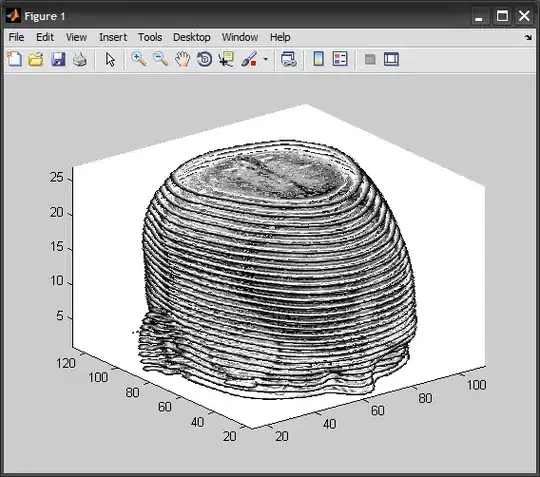
I have a set of 100 2-D image slices of the same size. I have used MATLAB to stack them to create a volumetric data. While the size of the 2-D slices is 480x488 pixels, the direction in which the images are stacked is not wide enough to visualize the volume in different orientation when projected. I need to interpolate along the slices to increase the size for visualization.
Can somebody please give me an idea or tip about how to do it?
Edit: Anotated projected microscopy-images


The figure 1 is the top-view of the projected volume.
The figure 2 is the side-view of the projected volume.
When I change the rotation-angle, and try to visualize the volume in different orientation, e.g. side-view (figure 2), is what I see as in figure 2.
I want to expand the side view by interpolating along the image slices.