I was looking at a question that was talking about a bad implementation of the Fisher-Yates shuffling algorithm and I was perplexed that there was a bias when implemented incorrectly.
The two algorithms are these:
private Random _random = new Random();
public int[] FisherYates(int[] source)
{
int[] output = source.ToArray();
for (var i = 0; i < output.Length; i++)
{
var j = _random.Next(i, output.Length);
(output[i], output[j]) = (output[j], output[i]);
}
return output;
}
public int[] FisherYatesBad(int[] source)
{
int[] output = source.ToArray();
for (var i = 0; i < output.Length; i++)
{
var j = _random.Next(0, output.Length);
(output[i], output[j]) = (output[j], output[i]);
}
return output;
}
A really subtle different, but enough to cause a massive bias.
Good implementation:
Bad implementation:
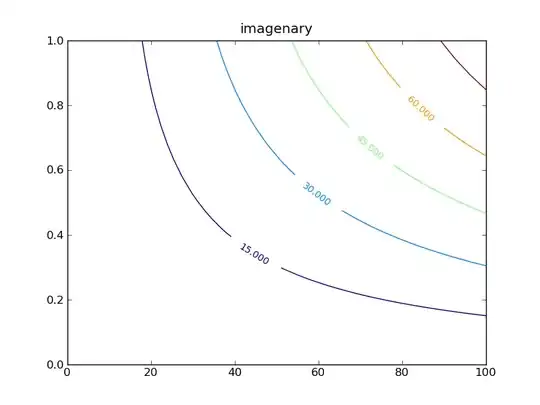
To be clear about these plots, I start with the numbers 0 to 99, create 10_000_000 shuffles using whichever algorithm and then I average the values in each of the shuffles to get a single set of figures. If the shuffle is trying random then all 100 figures would belong to the same normal distribution.
Now, that's all fine, but I thought I'd check to see if these methods produce valid results:
public int[] OrderByRandomNext(int[] source) => source.OrderBy(x => _random.Next()).ToArray();
public int[] OrderByRandomNextDouble(int[] source) => source.OrderBy(x => _random.NextDouble()).ToArray();
Both nice a neat, but are they a fair shuffle?
OrderByRandomNext:
OrderByRandomNextDouble:
Notice that the 1 and the 100 figures are significantly lower in each?
Well, I thought it might be an artefact of how OrderBy works. So I tested it with another random number generator - one brought to use from Eric Lippert in his improving Random series.
public int[] OrderByBetterRandomNextDouble(int[] source) => source.OrderBy(x => BetterRandom.NextDouble()).ToArray();
public static class BetterRandom
{
private static readonly ThreadLocal<RandomNumberGenerator> crng =
new ThreadLocal<RandomNumberGenerator>(RandomNumberGenerator.Create);
private static readonly ThreadLocal<byte[]> bytes =
new ThreadLocal<byte[]>(() => new byte[sizeof(int)]);
public static int NextInt()
{
crng.Value.GetBytes(bytes.Value);
return BitConverter.ToInt32(bytes.Value, 0) & int.MaxValue;
}
public static double NextDouble()
{
while (true)
{
long x = NextInt() & 0x001FFFFF;
x <<= 31;
x |= (long)NextInt();
double n = x;
const double d = 1L << 52;
double q = n / d;
if (q != 1.0)
return q;
}
}
}
Well, here's the chart:
There's no bias!
Here's my code to generate the data (run in LINQPad):
void Main()
{
var n = 100;
var s = 1000000;
var numbers = Enumerable.Range(0, n).ToArray();
var algorithms = new Func<int[], int[]>[]
{
FisherYates,
OrderByRandomNext,
OrderByRandomNextDouble,
OrderByBetterRandomNextDouble,
};
var averages =
algorithms
.Select(algorithm =>
Enumerable
.Range(0, numbers.Length)
.Select(x =>
Enumerable
.Range(0, s)
.Select(y => algorithm(numbers))
.Aggregate(0.0, (a, v) => a + (double)v[x] / s))
.ToArray())
.Select(x => new
{
averages = x,
distribution = Accord.Statistics.Distributions.Univariate.NormalDistribution.Estimate(x.Skip(1).SkipLast(1).ToArray()),
first = x.First(),
last = x.Last(),
})
.Select(x => new
{
x.averages,
x.distribution,
x.first,
x.last,
first_prob =x.distribution.DistributionFunction(x.first),
last_prob = x.distribution.DistributionFunction(x.last),
})
.ToArray();
var d =
averages.Dump();
}
private Random _random = new Random();
public int[] FisherYates(int[] source)
{
int[] output = source.ToArray();
for (var i = 0; i < output.Length; i++)
{
var j = _random.Next(i, output.Length);
(output[i], output[j]) = (output[j], output[i]);
}
return output;
}
public int[] OrderByRandomNext(int[] source) => source.OrderBy(x => _random.Next()).ToArray();
public int[] OrderByRandomNextDouble(int[] source) => source.OrderBy(x => _random.NextDouble()).ToArray();
public int[] OrderByBetterRandomNextDouble(int[] source) => source.OrderBy(x => BetterRandom.NextDouble()).ToArray();
public static class BetterRandom
{
private static readonly ThreadLocal<RandomNumberGenerator> crng =
new ThreadLocal<RandomNumberGenerator>(RandomNumberGenerator.Create);
private static readonly ThreadLocal<byte[]> bytes =
new ThreadLocal<byte[]>(() => new byte[sizeof(int)]);
public static int NextInt()
{
crng.Value.GetBytes(bytes.Value);
return BitConverter.ToInt32(bytes.Value, 0) & int.MaxValue;
}
public static double NextDouble()
{
while (true)
{
long x = NextInt() & 0x001FFFFF;
x <<= 31;
x |= (long)NextInt();
double n = x;
const double d = 1L << 52;
double q = n / d;
if (q != 1.0)
return q;
}
}
}
Here's the data that I generated:
distribution | first | last | first_prob | last_prob -------------------------------------------------------- | ------------------ | ------------------ | ---------------------- | --------------------- N(x; μ = 49.50267467345823, σ² = 0.0008896228453062147) | 49.505465999987585 | 49.49833699998965 | 0.5372807100387846 | 0.44218570467529394 N(x; μ = 49.50503062243786, σ² = 0.0009954477334487531) | 49.36330799998817 | 49.37124399998651 | 3.529550818615057E-06 | 1.115772521409486E-05 N(x; μ = 49.505720877539765, σ² = 0.0008257970106087029) | 49.37231699998847 | 49.386660999990106 | 1.7228855271333998E-06 | 1.712972513601141E-05 N(x; μ = 49.49994663264188, σ² = 0.0007518765247716318) | 49.50191999998847 | 49.474235999989205 | 0.5286859991636343 | 0.17421285127499514
Here's my question. What's up with System.Random and the bias it introduces?