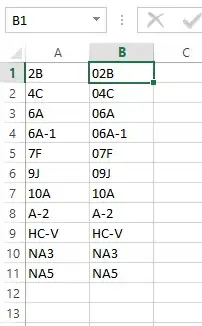
As previously mentioned in the comments, there are a couple of things be aware of:
- interpolating more than necessary
- correctly mapping the lerp
t parameter for interpolation (div in your code)
Regarding interpolation, your code currently has this section:
a1=lerp(x1, x2, div);
b1=lerp(y1, y2, div);
a2=lerp(x2, x3, div);
b2=lerp(y2, y3, div);
a3=lerp(x3, x1, div);
b3=lerp(y3, y1, div);
a4=lerp(x1, x2, div+div);
b4=lerp(y1, y2, div+div);
a5=lerp(x2, x3, div+div);
b5=lerp(y2, y3, div+div);
a6=lerp(x3, x1, div+div);
b6=lerp(y3, y1, div+div);
a7=lerp(x1, x2, div+div+div);
b7=lerp(y1, y2, div+div+div);
a8=lerp(x2, x3, div+div+div);
b8=lerp(y2, y3, div+div+div);
a9=lerp(x3, x1, div+div+div);
b9=lerp(y3, y1, div+div+div);
line(a1, b1, a2, b2);
line(a2, b2, a3, b3);
line(a3, b3, a1, b1);
line(a4, b4, a5, b5);
line(a5, b5, a6, b6);
line(a6, b6, a4, b4);
line(a7, b7, a8, b8);
line(a8, b8, a9, b9);
line(a9, b9, a7, b7);
The first 6 interpolations (between the 3 points of the triangle) deal with one subdivision level. Rendering lines using a1,a2,a3,b1,b2,b3,c1,c2,c3 should do the trick. The rest of the interpolation seem to be manually interpolating at another subdivision level. This is bit copy/pasted manual labour you would want to avoid and improve with a for loop.
Regarding the interpolation parameter if you know the total number of subdivisions you can map it to the t parameter either manually (using division) or making use of the map() function
Here's a modified version of your code to illustrate these points:
float x1, y1, x2, y2, x3, y3;
float b, a;
float a1, b1, a2, b2, a3, b3;
void setup () {
frameRate(10);
size(600, 600);
background(255);
x2=50;
y2=height-50;
x3=width-50;
y3=y2;
b=x3-x2;
a=b*sqrt(3)/2;
x1=x2+b/2;
y1=y2-a;
}
void draw() {
background(255);
int subdivisions = frameCount % 300;
for(float n = 1; n < subdivisions; n++){
float div= n / (subdivisions - 1);
a1=lerp(x1, x2, div);//x1x2
b1=lerp(y1, y2, div);//y1y2
a2=lerp(x2, x3, div);//x2x3
b2=lerp(y2, y3, div);//y2y3
a3=lerp(x3, x1, div);//x3x1
b3=lerp(y3, y1, div);//y3y1
stroke(255, 0, 153);
line(a1, b1, a2, b2);//x1x2,y1y2,x2x3,y2y3
stroke(0, 255, 253);
line(a3, b3, a1, b1);//x3x1,y3y1,x1x2,y1y2
stroke(79, 144, 252);
line(a2, b2, a3, b3);//x2x3,y2y3,x3x1,y3y1
}
}
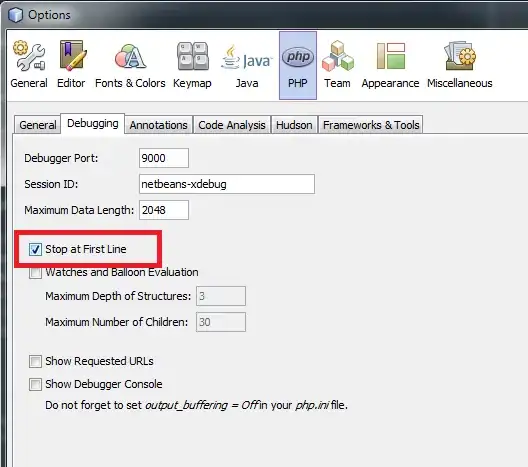
Personally I'd encapsulate it all in a reusable function (which would make it easier to reuse in other sketches). Here's an example where I'm also grouping all the line drawings in one go as oppose to multiple line() calls. This is a matter of preference mostly and should speed things up a tiny bit, however you should never sacrifice readability/flexibility easily.
float x1, y1, x2, y2, x3, y3;
float b, a;
color c1 = color(255, 0, 153);
color c2 = color(0, 255, 253);
color c3 = color(79, 144, 252);
void setup () {
size(600, 600);
background(255);
x2 = 50;
y2 = height - 50;
x3 = width - 50;
y3 = y2;
b = x3 - x2;
a = b * sqrt(3) / 2;
x1 = x2 + b / 2;
y1 = y2 - a;
}
void drawSubdivisions(int div, float x1, float y1,
float x2, float y2,
float x3, float y3,
color c1, color c2, color c3){
// alternative rendering option: render the lines in a batch
beginShape(LINES);
// for each subdivision level
for(int i = 0; i < div; i++){
// map the subdivision level to the t interpolation parameter
float t = map(i, 0, div - 1, 0.0, 1.0);
// interpolate each coordinate
// connecting the current triangle vertex to the next
float x1x2 = lerp(x1, x2, t);
float y1y2 = lerp(y1, y2, t);
float x2x3 = lerp(x2, x3, t);
float y2y3 = lerp(y2, y3, t);
// ... and last vertex to first vertex
float x3x1 = lerp(x3, x1, t);
float y3y1 = lerp(y3, y1, t);
// render lines for th interpolated shape
stroke(c1);
vertex(x1x2, y1y2);
vertex(x2x3, y2y3);
stroke(c2);
vertex(x2x3, y2y3);
vertex(x3x1, y3y1);
stroke(c3);
vertex(x3x1, y3y1);
vertex(x1x2, y1y2);
}
endShape();
}
void draw() {
// map the number of subdivisions
int subdivisions = round(map(mouseX, 0, width, 2, 90));
background(0);
drawSubdivisions(subdivisions, x1, y1, x2, y2, x3, y3, c1, c2, c3);
text("move mouse on X axis to control subdivisions: " + subdivisions, 10, 15);
}
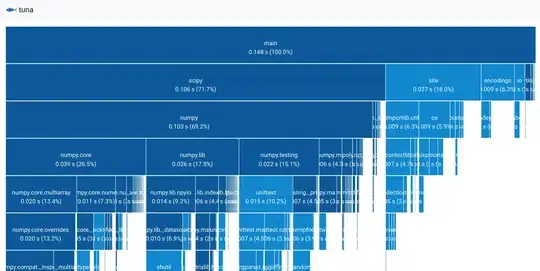
For the sake of completeness here's an example written in p5.js which you can run bellow. I generalises the equilateral triangle to regular polygons and plays with colour mapping:
function setup() {
createCanvas(900, 900);
colorMode(HSB, 360, 100, 100);
}
function draw() {
background(0, 0, 100);
// map the number of points to Y axis
let numPoints = round(map(mouseY, 0, height, 3, 6));
// map the number of subdivisions to the X axis
let subdivisions = round(map(mouseX, 0, width, 1, 300));
// compute regular polygon points
let regularPolygonPoints = getRegularPolygonPoints(width * 0.5, height * 0.5, numPoints, 300);
// optional: render regular polygon points
if(mouseIsPressed) drawPoints(regularPolygonPoints);
// compute and render interpolation lines between pairs of points
drawLinearInterpolation(regularPolygonPoints, subdivisions);
// instructions:
text(`mouseY -> numPoints:${numPoints}\nmouseX -> subdivisions: ${subdivisions}`, 10, 15);
}
// make a list of points (p5.Vector with x, y properties and conveniently lerp)
function getRegularPolygonPoints(x, y, sides, radius){
// output list
let points = [];
// calculate the angle per polygon side (same as 360 degrees / sides)
let angleIncrement = TWO_PI / sides;
// for each side
for(let i = 0 ; i < sides; i++){
// increment the angle (and offset by 90 degrees to point up)
let angle = (angleIncrement * i) - HALF_PI;
// insert the points into the list
// p5.Vector.fromAngle converts and angle radius to an x and y position (polar to cartesian)
// we offset(add) by x, y (transalation from 0,0 to center)
points.push(p5.Vector.fromAngle(angle, radius).add(x, y));
}
// return result
return points;
}
// draw lines between interpolated pairs of points in sequental side order
function drawLinearInterpolation(points, subdivisions){
// make strokes thinner the more subdivisions there are
strokeWeight((300 - subdivisions) / 600);
let numPoints = points.length;
beginShape(LINES);
// for each subdivision
for(let i = 0; i < subdivisions; i++){
let amount = map(i, 0, subdivisions - 1, 0.0, 1.0);
// for each point index from first to last (and back to first)
for(let j = 0; j <= numPoints; j++){
// array access current, previous and next points
let current = points[j % numPoints];
let previous = points[(j-1) < 0 ? numPoints - 1 : j - 1];
let next = points[(j+1) % numPoints];
// interpolate between pairs of points: previous to current, current to next
let previousToCurrent = p5.Vector.lerp(previous, current, amount);
let currentToNext = p5.Vector.lerp(current, next, amount);
// play with stroke colour mapping
stroke((mouseIsPressed ? (i + j) : (i * j)) % 360, 85, 100);
// pass the point coordinates for shape rendering
vertex(previousToCurrent.x, previousToCurrent.y);
vertex(currentToNext.x, currentToNext.y);
}
}
endShape();
}
// render a list of points
function drawPoints(points){
strokeWeight(9);
stroke(0, 100, 0);
let numPoints = points.length;
beginShape(POINTS);
for(let i = 0 ; i < numPoints; i++){
let point = points[i];
vertex(point.x, point.y);
}
endShape();
}
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/1.3.1/p5.min.js"></script>
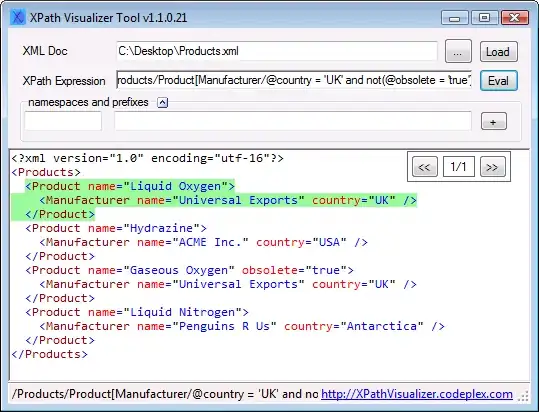
You may choose to use a different colour mapping. Functions like lerpColor() and colorMode() may be useful. Have fun!