Multiply two variables in an objective function using cvxr

Question

I want to minimize the following objective function

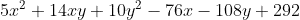
with some constraints

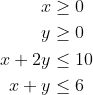
And another user (I think it was G. Grothendieck) suggested to use the CVXR package of R.

So I followed the instructions on A Gentle Introduction to CVXR to make my code

library(CVXR)  # if necessary
x <- Variable(1)
y <- Variable(1)
objective <- Minimize(5*x^2 + 14*x*y + 10*y^2 -76*x -108*y +292)
constraints <- list(x >= 0, y >= 0, x + 2*y <=10, x + y<=6)
prob_OF <- Problem(objective, constraints)
solution_OF <- solve(prob_OF)  # and here the error occured

## Error in construct_intermediate_chain(object, candidate_solvers, gp = gp): Problem does not follow DCP rules.

On How to convert quadratic to linear program? I found the hint to the McCormick envelopes that helps to solve the issue with the bilinear formular part 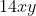. Especially the 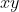part.

At the end of the answer of josliber he remarks, that all the variables should have a bound. In my constraints there is no upper bound and therefore I insert an upper bound. It's an arbitrary choice. You have to recalculate with new bounds if the solution is on the bound...

library(CVXR)  # if necessary
x <- Variable(1)
y <- Variable(1)
w <- Variable(1)
objective <- Minimize(5*x^2 + 14*w + 10*y^2 -76*x -108*y +292)
constraints <- list(x >= 0, x <= 100,
                    y >= 0, y <= 100,
                    x+2*y <= 10, 
                    x+y <= 6,
                    w >= 0, w >= 100*x + 100*y - 10000,  # constraints according to McCormick envelopes
                    w <= 100*y, w <= 100*x)  # constraints according to McCormick envelopes
prob_OF <- Problem(objective, constraints)
solution_OF <- solve(prob_OF)
solution_OF$value
## -125.0667
solution_OF$getValue(x)                  
## 2.933333
solution_OF$getValue(y)
## 3.066667
solution_OF$getValue(w)
## 1.000135e-30

Here the solution is not my expected one... When I solve the same objective function with solve.QP() then I get and . For establishing the code look at my other question...

Let's check the code:

# Parameters of the objective funtion and the constraints
D=matrix(c(5,7,7,10),ncol=2,byrow=TRUE)
d=c(-78,-108)
A=matrix(c(1,2,1,1),ncol=2,byrow=TRUE)
b=c(10,6)

# Convert the parameters to an appropriate state of solve.QP()
Dmat=2*D
dvec=-d
Amat=-t(A)
bvec=-b

# load the package and run solve.QP()
library(quadprog)
solve.QP(Dmat,dvec,Amat,bvec,meq=0,factorized=TRUE)
## $solution
## [1] 2 4     # these are the x and y results
##
## $value
## -587.9768
##
## and some more results...

Question:

• Why are the two results different?
  • In which of the solving alternatives I have done any mistakes? Is it possible to point them out?
• And when I put in the x and y from the results I don't get the $value of the solve.QP() alternatives
  • When doing the math
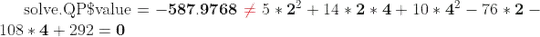
  • And as you can see the results don't coincide
  • Am I doing here an mistake?!

Many thanks in advance!

Answer 1

The problems are that

1. the question is using factorized=TRUE
2. the objective function at the top of the question implies a different dvec[1] than shown in the code in the question.

If we omit factorized (default is FALSE) and consistently use the code in the question that defines Dmat, dvec, Amat and bvec then we get consistent results from solve.QP and manually computing the objective based on the solution vector, both being -297. The code until ###### is copied verbatim from the question.

# Parameters of the objective funtion and the constraints
D=matrix(c(5,7,7,10),ncol=2,byrow=TRUE)
d=c(-78,-108) 
A=matrix(c(1,2,1,1),ncol=2,byrow=TRUE)
b=c(10,6)

# Convert the parameters to an appropriate state of solve.QP()
Dmat=2*D
dvec=-d
Amat=-t(A)
bvec=-b

######

library(quadprog)
ans <- solve.QP(Dmat,dvec,Amat,bvec)
str(ans)
## List of 6
##  $ solution              : num [1:2] 3 3
##  $ value                 : num -297
##  ...snip...

# manual calculation of objective function
t(ans$solution) %*% Dmat %*% ans$solution / 2 - dvec %*% ans$solution
##      [,1]
## [1,] -297

# another manual calculation - coefficients come from Dmat and dvec
f <- function(x, y) (10 * x^2 + 2 * 14 * x * y + 20 * y^2) / 2 - (78 * x + 108 * y)
f(3, 3)
## [1] -297