Your question includes two separate stages:
- Alignment
- Overlaying the plotted images.
Let's get #2 out of our way, because using matplotlib's pyplot.imshow you can just plot them out on the same axis and use the alpha input for controlling transparency/opacity, or otherwise use cv2's overlay option -
import cv2
im1_ = im1.copy()
im2_ = im2.copy()
cv2.addWeighted(im1_, 0.5, im2_, 0.5, 0, im2_)
cv2.imshow("Overlay", output)
Regarding alignment (which is the more complex issue by far), you need to "process" one of the images such that it's best matched to the other. This might be one of many optional mappings such as translation, rotation, homographic mapping, and more.
A first point to note is that your matches do not agree with each other as far as only shifts are involved. In other words, if we were to consider only a 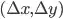 global shift, then the first matching estimates a shift of (15, 16), while the second matching estimates a shift of (-6, -5). Depending on the fidelity of the required image-fitting, it might suffice to just average these two estimates and translate the image accordingly.
global shift, then the first matching estimates a shift of (15, 16), while the second matching estimates a shift of (-6, -5). Depending on the fidelity of the required image-fitting, it might suffice to just average these two estimates and translate the image accordingly.
If that's not enough, then you're implicitly assuming there's some more complex mapping or warping going on, and these mappings generally require more than two points for estimating their parameters. (I think the maximum you can do with two points is "similarity", which includes a combination of translation, rotation, and scale).
On a more general note, maybe you want to consider matching them using opencv functions, for finding keypoints (via SIFT for instance) and/or for finding the actual mapping. See this example tutorial, although there are other, more direct methods that don't require going explicitly through keypoints. This is a good starting point on using ECC (Enhanced Correlation Coefficient).
More specifically, if you have enough points, you can use cv2.findHomography which accepts lists of key-points as inputs.
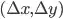 global shift, then the first matching estimates a shift of (15, 16), while the second matching estimates a shift of (-6, -5). Depending on the fidelity of the required image-fitting, it might suffice to just average these two estimates and translate the image accordingly.
global shift, then the first matching estimates a shift of (15, 16), while the second matching estimates a shift of (-6, -5). Depending on the fidelity of the required image-fitting, it might suffice to just average these two estimates and translate the image accordingly.