Create matrix out of list with mathematica

Question

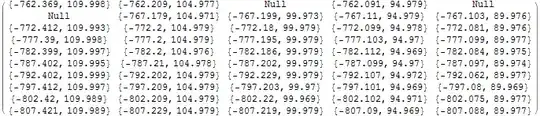
I have a problem which I try to solve with mathematica. I am having a list with x and y coordinates from a position measurement (and also with z values of the quantity which was measured at each point). So, my list starts with list={{-762.369,109.998,0.915951},{-772.412,109.993,0.923894},{-777.39, 109.998, 0.918108},...} (x,y,z). Out of some reasons, I have to fill all these x,y, and z-values into a matrix. That would be easy if I have for each y-coordinate the same amount of x-coordinates (lets say 80), then I could use Partition[list,80] which produces a matrix with 80 columns (and some rows whose number is given by the number of y-coordinates with the same value).
Unfortunately, it is not so easy, the number of x-coordinates for each y is not strictly constant, as can be seen from the attached ListPlot. Can anybody give me some suggestions, how I could fill each point of this plot / each x-y-(and z-) coordinate of my list into a matrix?

To explain better what I want to have, I indicated in the attached picture a matrix. There one can see that almost every point of my plot would fall into a cell of a matrix, only some cells would stay empty. I used in the plot the color red for the points whose x coordinates are ascending in my list and blue for the points whose x coordinate are descending in my list (the positions are measured along a meander line). Perhaps this kind of order can be useful to solve to problem... Here a link to my coordinates, perhaps this helps.

Well, I hope I explained my question well enough. I would appreciate every help much!

Answer 1

The basic idea behind this solution is:

• all points seem to lie on a lattice, but it's not precisely a square lattice (it's slanted)
• so let's find the basis vectors of the lattice, then all (most?) points will be approximate integer linear combinations of the basis vectors
• the integer "coordinates" of the points along the basis vectors will be the matrix indices for the OP's matrix

(The OP emailed me the datafile. It consists of {x,y} point coordinates.)

Read in the data:

data = Import["xy.txt", "Table"];

Find the nearest 4 points to each point, and notice that they lie about distance 5 away both horizontally and vertically:

nf = Nearest[data];

In:= # - data[[100]] & /@ nf[data[[100]], 5]

Out= {{0., 0.}, {-4.995, 0.}, {5.003, 0.001}, {-0.021, 5.003}, {0.204, -4.999}}

ListPlot[nf[data[[100]], 5], PlotStyle -> Red, 
  PlotMarkers -> Automatic, AspectRatio -> Automatic]

Generate the difference vectors between close points and keep only those that are about length 5:

vv = Select[
      Join @@ Table[(# - data[[k]] & /@ nf[data[[k]], 5]), {k, 1, Length[data]}], 
      4.9 < Norm[#] < 5.1 &
     ];

Average the vectors out by directions they can point to, and keep two "good" ones (pointing "up" or to the "right").

In:= Mean /@ GatherBy[vv, Round[ArcTan @@ #, 0.25] &]

Out= {{0.0701994, -4.99814}, {-5.00094, 0.000923234}, {5.00061, -4.51807*10^-6},  
      {-4.99907, -0.004153}, {-0.0667469, 4.9983}, {-0.29147, 4.98216}}

In:= {u1, u2} = %[[{3, 5}]]

Out= {{5.00061, -4.51807*10^-6}, {-0.0667469, 4.9983}}

Use one random point as the point of origin, so the coordinates along the basis vectors u1 and u2 will be integers:

translatedData = data[[100]] - # & /@ data;

Let's find the integer coordinates and see how good they are (how far they are from actual integers):

In:= integerIndices = LinearSolve[Transpose[{u1, u2}], #] & /@ translatedData ;

In:= Max[Abs[integerIndices - Round[integerIndices]]]

Out= 0.104237

In:= ListPlot[{integerIndices, Round[integerIndices]}, PlotStyle -> {Black, Red}]

All points lie close to the integer approximations.

Offset the integer coordinates so they're all positive and can be used as matrix indices, then gather the elements into a matrix. I put the coordinates in a point object in order not to confuse SparseArray:

offset = Min /@ Transpose[Round[integerIndices]]
offset = {1, 1} - offset

result = 
 SparseArray[
  Thread[(# + offset & /@ Round[integerIndices]) -> point @@@ data]]

result = Normal[result] /. {point -> List, 0 -> Null}

And we finally have a matrix result where each element is a coordinate-pair! (I was sloppy doing 0 -> Null here to mark missing elements: it's important that data contained no exact 0s.)

MatrixForm[result[[1 ;; 10, 1 ;; 5]]]

EDIT

Just for fun, let's look at the deviations of points from the precise integer lattice sites:

lattice = #1 u1 + #2 u2 & @@@ Round[integerIndices];

delta = translatedData - lattice;
delta = # - Mean[delta] & /@ delta;

ListVectorPlot[Transpose[{lattice, delta}, {2, 1, 3}], VectorPoints -> 30]