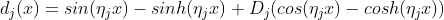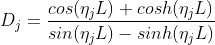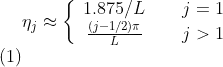Numpy returns unexpected results of analytical function

Question

When I try to compute d_j(x), defined below, the algorithm based on Numpy results in unexpected values. I believe it has something to do with numerical precision, but I'm not sure how to solve this.

The function is:

latex equation

where

latex equation

and

latex equation

The code fails when j>10. For example, when j=16, the function d_j(x) returns wrong values from around x=1, while the expected result is a smooth, almost periodic curve.

Graph for 0<x<1.5:

The code is:

#%%
import numpy as np
import matplotlib.pyplot as plt

#%%
L = 1.5  # Length [m]

def eta(j):
    if j == 1:
        return 1.875 / L
    if j > 1:
        return (j - 0.5) * np.pi / L


def D(etaj):
    etajL = etaj * L
    return (np.cos(etajL) + np.cosh(etajL)) / (np.sin(etajL) - np.sinh(etajL))


def d(x, etaj):
    etajx = etaj * x
    return np.sin(etajx) - np.sinh(etajx) + D(etaj) * (np.cos(etajx) - np.cosh(etajx))


#%%
aux = np.linspace(0, L, 2000)
plt.plot(aux, d(aux, eta(16)))
plt.show()

'gets lost', 'fails', and 'messy' are useless problem descriptors. [mcve] — hpaulj, Jul 26 '21 at 22:35

score 7 · Accepted Answer · answered Jul 26 '21 at 22:38

TL;DR: The problem comes from numerical instabilities.

First of all, here is a simplified code on which the exact same problem appear (with different values):

x = np.arange(0, 50, 0.1)
plt.plot(np.sin(x) - np.sinh(x) - np.cos(x) + np.cosh(x))
plt.show()

Here is another example where the problem does not appear:

x = np.arange(0, 50, 0.1)
plt.plot((np.sin(x) - np.cos(x)) + (np.cosh(x) - np.sinh(x)))
plt.show()

While the two code are mathematically equivalent with real numbers, they are not equivalent because of fixed-size floating-point precision. Indeed, np.sinh(x) and np.cosh(x) result both in huge values when x is big compared to np.sin(x) and np.cos(x). Unfortunately, when two fixed-size floating-point numbers are added together, there is a loss of precision. The loss of precision can be huge (if not critical) when the order of magnitude of the added numbers are very different. For example, in Python and on a mainstream platform (so with IEEE-754 64-bit floating-point numbers), 0.1 + 1e20 == 1e20 is true due to the limited precision of the number representation. Thus (0.1 + 1e20) - 1e20 == 0.0 is also true, while 0.1 + (1e20 - 1e20) == 0.0 is not true (the resulting value is 0.1). The floating-point addition is neither associative nor commutative. In this specific case, the accuracy can reach a threshold where there is not significant number anymore in the result. For more information about floating-point precision, please read this post.

The point is you should be very careful when you subtract floating-point numbers. A good solution is to put parenthesis so that added/subtracted values have the same order of magnitude. Variable-sized and higher precision help a bit too. However, the best solution is to analyses the numerical stability of your algorithm. For example, studying condition number of the numerical operations used in your algorithm is a good start.

Here, a relatively good solution is just to use the second code instead of the first.

That was it, thanks for taking the time to elaborate! Based on your sugestion I went a little further and used the hyperbolic funcions definitions to replaced the expression by `np.sin(etajx) + D(etaj)*np.cos(etajx) - 0.5*((D(etaj) - 1)*np.exp(-etajx) + (D(etaj) + 1)*np.exp(etajx))`, since there still was small errors when using np.sinh() — Schroeder, Jul 27 '21 at 14:14

score 2 · Answer 2 · answered Jul 27 '21 at 11:55

2

using:

aux = np.linspace(0, L, 2000).astype(np.longdouble)

it gets better for a little bit

answered Jul 27 '21 at 11:55

pippo1980

2,181
3
14
30

It definitivaly helps. Combined with @Jérôme Richard answer, it's a powerfull way to avoid numerical instabilities, thank you! – Schroeder Jul 27 '21 at 14:18

Numpy returns unexpected results of analytical function

2 Answers2