Take some data, return a pure piecewise function

Question

Given a list of {x,y} datapoints, return a pure function f (from the reals to the reals) such that f[x]==y for every {x,y} in the data. If x is not one of the x-values then return the y-value for the previous point (the one with x-value less than x). If the function gets a value less than that of the first x-value in the data -- i.e., there is no previous point -- then return 0.

For example, given data {{1,20}, {2,10}}, return a pure function that looks like this:

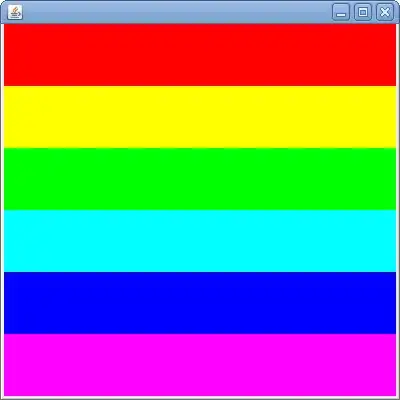
Graph of the function given {{1,20},{2,10}} http://yootles.com/outbox/so/piecewise.png

I wrote something using Function and Piecewise that I'll include as an answer but it seems like it might be inefficient, especially for a large list of points. [UPDATE: My answer may actually be decent now. I'll probably go with it if no one has better ideas.]

To be clear, we're looking for function that takes a single argument -- a list of pairs of numbers -- and returns a pure function. That pure function should take a number and return a number.

Answer 1

Hand-Coded Binary Search

If one is willing to sacrifice conciseness for performance, then an imperative binary search approach performs well:

stepifyWithBinarySearch[data_] :=
  With[{sortedData = SortBy[data, First], len = Length @ data}
  , Module[{min = 1, max = len, i, x, list = sortedData}
    , While[min <= max
      , i = Floor[(min + max) / 2]
      ; x = list[[i, 1]]
      ; Which[
          x == #, min = max = i; Break[]
        , x < #, min = i + 1
        , True, max = i - 1
        ]
      ]
    ; If[0 == max, 0, list[[max, 2]]]
    ]&
  ]

Equipped with some test scaffolding...

test[s_, count_] :=
  Module[{data, f}
  , data = Table[{n, n^2}, {n, count}]
  ; f = s[data]
  ; Timing[Plot[f[x], {x, -5, count + 5}]]
]

...we can test and time various solutions:

test[stepifyWithBinarySearch, 10]

On my machine, the following timings are obtained:

test[stepify (*version 1*), 100000]      57.034 s
test[stepify (*version 2*), 100000]      40.903 s
test[stepifyWithBinarySearch, 100000]     2.902 s

I expect that further performance gains could be obtained by compiling the various functions, but I'll leave that as an exercise for the reader.

Better Still: Precomputed Interpolation (response To dreeves' comment)

It is baffling that a hand-coded, uncompiled binary search would beat a Mathematica built-in function. It is perhaps not so surprising for Piecewise since, barring optimizations, it is really just a glorified IF-THEN-ELSEIF chain testing expressions of arbitrary complexity. However, one would expect Interpolation to fare much better since it is essentially purpose-built for this task.

The good news is that Interpolation does provide a very fast solution, provided one arranges to compute the interpolation only once:

stepifyWithInterpolation[data_] :=
  With[{f=Interpolation[
            {-1,1}*#& /@ Join[{{-9^99,0}}, data, {{9^99, data[[-1,2]]}}]
            , InterpolationOrder->0 ]}
    , f[-#]&
  ]

This is blindingly fast, requiring only 0.016 seconds on my machine to execute test[stepifyWithInterpolation, 100000].

Answer 2

You could also do this with Interpolation (with InterpolationOrder->0) but that interpolates by using the value of the next point instead of the previous. But then I realized you can reverse that with a simple double-negation trick:

stepify[data_] := Function[x,
  Interpolation[{-1,1}*#& /@ Join[{{-9^99,0}}, data, {{9^99, data[[-1,2]]}}],
                InterpolationOrder->0][-x]]

Answer 3

My previous attempts were not working properly (they were OK for two steps only).

I think the following one, along the same lines, works:

g[l_] := Function[x, 
  Total[#[[2]] UnitStep[x - #[[1]]] & /@ 
    Transpose@({First@#, Differences[Join[{0}, Last@#]]} &@ Transpose@l)]]

Plot[g[{{1, 20}, {2, 10}, {3, 20}}][x], {x, 0, 6}]

Answer 4

Compiling WReach's answer does indeed result in a significant speedup. Using all the functions defined in WReach's answer, but redefining test to

test[s_,count_]:=Module[{data,f},
    data=Table[{n,n^2},
        {n,count}];
        f=s[ToPackedArray[N@data]];
        Timing[Plot[f[x],{x,-5,count+5}]]]

(this is necessary to force the resulting arrays to be packed; thanks to Sjoerd de Vries for pointing this out), and defining

ClearAll[stepifyWRCompiled];
stepifyWRCompiled[data_]:=With[{len=Length@data,sortedData=SortBy[data,First]},
Compile[{{arg,_Real}},Module[{min=1,max=len,i,x,list=sortedData},
            While[
                min<=max,
                i=Floor[(min+max)/2];
                    x=list[[i,1]];
                    Which[
                        x\[Equal]arg,min=max=i;Break[],
                        x<arg,min=i+1,True,max=i-1
                    ]
            ];
            If[0==max,0,list[[max,2]]]
        ],CompilationTarget->"WVM",RuntimeOptions\[Rule]"Speed"]]

(the With block is necessary to explicitly insert sortedData into the block of code to be compiled) we get results faster even than the solution using Interpolation, although only marginally so:

Monitor[
tbl = Table[
    {test[stepifyWRCompiled, l][[1]],
        test[stepifyWithInterpolation, l][[1]],
        test[stepifyWithBinarySearch, l][[1]]},
        {l, 15000, 110000, 5000}], l]
tbl//TableForm
(*
0.002785    0.003154    0.029324
0.002575    0.003219    0.031453
0.0028      0.003175    0.034886
0.002694    0.003066    0.034896
0.002648    0.003002    0.037036
0.00272     0.003019    0.038524
0.00255     0.00325     0.041071
0.002675    0.003146    0.041931
0.002702    0.003044    0.045077
0.002571    0.003052    0.046614
0.002611    0.003129    0.047474
0.002604    0.00313     0.047816
0.002668    0.003207    0.051982
0.002674    0.00309     0.054308
0.002643    0.003137    0.05605
0.002725    0.00323     0.06603
0.002656    0.003258    0.059417
0.00264     0.003029    0.05813
0.00274     0.003142    0.0635
0.002661    0.003023    0.065713
*)

(first column is compiled binary search, second interpolation, third, uncompiled binary search).

Note also that I use CompilationTarget->"WVM", rather than CompilationTarget->"C"; this is because the function is compiled with a lot of data points "built-in", and, if I use compilation to C with 100000 data points, I can see that gcc goes on for a long time and takes up a lot of memory (I imagine the resulting C file is huge, but I did not check). So I just use compilation to "WVM".

I think the overall conclusion here is just that Interpolation is also just doing some constant-time lookup (binary search or something similar, presumably) and the hand-coded way just happens to be slightly faster because it's less general.

Answer 5

The following works:

stp0[x_][{{x1_,y1_}, {x2_,y2_}}] := {y1, x1 <= x < x2}
stepify[{}] := (0&)
stepify[data_] := With[{x0 = data[[1,1]], yz = data[[-1,2]]},
  Function[x, Piecewise[Join[{{0, x<x0}}, stp0[x] /@ Partition[data, 2,1]], yz]]]

Note that without the With it will leave things like {{1,10},{2,20}}[[1,1]] in the returned function, which seems a little wasteful.

By the way, I decided to call this stepify since it turns a list of points into a step function.