How to calculate point spread function (PSF) for signal data?

Question

I have chromatograph data (signal) in a pandas df and in one of the signal processing step is to perform peak sharpening as shown in fig below

The reference literature is as follows:

Literature :Paper 1(Peak sharping section ) Paper 2

Algorithm in Literature

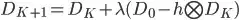
$D_{K+1} = D_{K} + \lambda(D_{0} - h\bigotimes_{}^{}D_{K})$

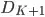$D_{K+1}$ : Deconvolved high resolution data after K + 1 iterations

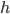: point spread function

Adaptive point spread function estimation: Peaks are detected in the regularized trace and called as bases with standard classification methods. The called peaks are used to adaptively estimate the local point spread function h. The time-localization parameter d is estimated according to the peak spacing in the segment.

How I can find h for signal data? Already gone through following

PSF (point spread function) for an image (2D)

How do you extract a point spread function from a fits image?

How to build a function in Python (Jupyter) for calculation of Point Spread Function (image processing?)

in all of these it was image data

Sample Data

Sample data
array([[ 31,  49,   1,  44],
       [ 36,  48,   0,  47],
       [ 43,  47,   0,  53],
       [ 50,  44,   0,  63],
       [ 59,  41,   0,  75],
       [ 68,  40,   1,  90],
       [ 78,  40,   6, 107],
       [ 87,  41,  12, 123],
       [ 99,  43,  20, 140],
       [110,  45,  31, 155],
       [121,  47,  42, 170],
       [131,  48,  53, 182],
       [140,  49,  63, 191],
       [148,  50,  72, 196],
       [155,  51,  79, 196],
       [161,  53,  83, 189],
       [166,  55,  83, 177],
       [169,  58,  80, 160],
       [170,  62,  72, 140],
       [167,  65,  62, 119],
       [161,  70,  51, 100],
       [154,  75,  40,  84],
       [144,  80,  30,  72],
       [132,  86,  23,  65],
       [121,  92,  19,  61],
       [111,  98,  19,  61],
       [106, 102,  23,  63],
       [105, 104,  29,  67],
       [111, 104,  38,  71],
       [123, 102,  48,  75],
       [141,  98,  59,  78],
       [160,  92,  71,  79],
       [179,  85,  85,  78],
       [195,  77, 101,  74],
       [205,  68, 117,  68],
       [208,  59, 133,  61],
       [203,  51, 145,  52],
       [191,  43, 152,  43],
       [173,  37, 154,  35],
       [150,  32, 151,  28],
       [123,  30, 142,  23],
       [ 94,  32, 129,  20],
       [ 65,  40, 114,  21],
       [ 40,  52,  96,  25],
       [ 21,  70,  77,  35],
       [  9,  91,  58,  51],
       [  1, 113,  39,  71],
       [  0, 134,  24,  97],
       [  0, 152,  13, 126],
       [  0, 168,   5, 157],
       [  0, 181,   0, 188],
       [  0, 193,   0, 216],
       [  0, 203,   0, 241],
       [  0, 211,   0, 258],
       [  0, 215,   0, 265],
       [  0, 213,   0, 262],
       [  0, 207,   0, 249],
       [  0, 195,   0, 227],
       [  0, 180,   0, 200],
       [  0, 164,   0, 170],
       [  0, 148,   0, 140],
       [  0, 132,   0, 113],
       [  0, 116,   0,  90],
       [  0, 100,   5,  74],
       [  0,  83,  18,  62],
       [  0,  66,  38,  57],
       [  0,  49,  64,  58],
       [  0,  36,  98,  64],
       [  0,  25, 133,  76],
       [  0,  18, 164,  94],
       [  0,  15, 187, 116],
       [  0,  16, 199, 143],
       [  0,  18, 199, 169],
       [  0,  22, 186, 193],
       [  1,  26, 164, 211],
       [  7,  28, 134, 222],
       [ 17,  29, 102, 224],
       [ 31,  28,  71, 218],
       [ 50,  26,  44, 204],
       [ 71,  22,  24, 184],
       [ 91,  18,  11, 160],
       [106,  13,   4, 134],
       [117,   8,   3, 109],
       [122,   5,   5,  85],
       [120,   2,  10,  64],
       [113,   0,  16,  46],
       [101,   0,  22,  32],
       [ 86,   0,  28,  22],
       [ 69,   0,  34,  16],
       [ 52,   3,  39,  13],
       [ 36,  10,  44,  13],
       [ 24,  22,  47,  18],
       [ 18,  37,  48,  25],
       [ 20,  56,  46,  36],
       [ 31,  76,  39,  49],
       [ 51,  94,  28,  63],
       [ 81, 110,  19,  75],
       [118, 123,  10,  85],
       [158, 132,   4,  90],
       [199, 136,   0,  89],
       [236, 135,   0,  84],
       [265, 131,   0,  73],
       [282, 122,   0,  59],
       [286, 110,   0,  44],
       [277,  95,   0,  29],
       [256,  79,   0,  17],
       [226,  61,   0,   8],
       [189,  44,   0,   2],
       [150,  29,   6,   0],
       [112,  17,  19,   0],
       [ 77,   8,  41,   0],
       [ 49,   3,  74,   0],
       [ 28,   0, 117,   0],
       [ 15,   0, 168,   3],
       [  7,   0, 224,  12],
       [  5,   0, 280,  28],
       [  5,   0, 333,  53],
       [  5,   0, 379,  87],
       [  5,   0, 411, 130],
       [  4,   0, 425, 178],
       [  2,   0, 419, 226],
       [  1,   0, 393, 271],
       [  0,   0, 350, 307],
       [  0,   0, 299, 329],
       [  0,   0, 248, 334],
       [  0,   0, 206, 320],
       [  0,   0, 178, 289],
       [  0,   0, 167, 246],
       [  0,   0, 173, 196],
       [  0,   0, 192, 146],
       [  0,   0, 217, 100],
       [  0,   0, 246,  61],
       [  0,   0, 275,  33],
       [  0,   0, 301,  15],
       [  0,   0, 326,   4],
       [  0,   0, 351,   0],
       [  0,   0, 377,   0],
       [  0,   0, 403,   0],
       [  0,   0, 430,   0],
       [  0,   0, 456,   0],
       [  0,   0, 484,   0],
       [  0,   0, 510,   0],
       [  0,   3, 535,   0],
       [  0,   7, 555,   0],
       [  0,  14, 569,   0],
       [  0,  22, 574,   0],
       [  0,  33, 572,   0],
       [  0,  44, 565,   0],
       [  0,  55, 555,   0],
       [  0,  66, 548,   0],
       [  1,  76, 546,   0],
       [  9,  84, 550,   0],
       [ 27,  91, 555,   0],
       [ 53,  94, 558,   0],
       [ 88,  95, 554,   0],
       [132,  94, 536,   2],
       [178,  91, 503,   7],
       [219,  86, 453,  15],
       [252,  82, 390,  24],
       [273,  77, 317,  36],
       [279,  72, 240,  44],
       [270,  69, 165,  49],
       [247,  69, 102,  48],
       [214,  73,  55,  41],
       [173,  83,  23,  30],
       [132,  98,   5,  19],
       [ 93, 121,   0,  10],
       [ 59, 150,   0,   3],
       [ 34, 186,   0,   0],
       [ 17, 227,   0,   0],
       [  6, 271,   0,   0],
       [  1, 315,   0,   0],
       [  0, 354,   0,   0],
       [  0, 384,   0,   5],
       [  0, 404,   0,  13],
       [  0, 413,   0,  25],
       [  0, 411,   0,  39],
       [  0, 398,   0,  55],
       [  0, 378,   0,  67],
       [  0, 350,   0,  75],
       [  0, 315,   0,  76],
       [  0, 276,   9,  72],
       [  0, 235,  28,  64],
       [  0, 198,  60,  53],
       [  2, 164, 107,  42],
       [ 13, 139, 172,  30],
       [ 36, 120, 242,  20],
       [ 78, 109, 310,  12],
       [143, 103, 367,   7],
       [233, 101, 404,   3],
       [344, 101, 414,   1],
       [467, 103, 394,   0],
       [591, 103, 350,   0],
       [702, 100, 287,   0],
       [786,  94, 215,   0],
       [831,  84, 144,   0],
       [833,  70,  86,   0],
       [792,  54,  44,   4],
       [713,  38,  17,  16],
       [606,  24,   4,  36]], dtype=int64)

What happens if you take the Fourier transform of your data - does the PSF jump out? — jtlz2, Jul 28 '21 at 09:11
I think we need 4 , for each column , yes data has noise as it is acquired from sequencing machines; hence a pre-processing stage is needed to achieve noise removal . I already have applied de-correlational (reduction of Cross-Talk effect) by using correlation matrix — alex3465, Jul 28 '21 at 10:40
You can keep the noise - it might help with the stability of the PSF fit. Can you post the noise vectors? — jtlz2, Jul 28 '21 at 10:41
I just followed the Paper 1, where pre-processing steps( Decorrelational, Peak Sharpening and Normalization ) were performed on raw data to extract features for ML model , I am trying to achieve similar — alex3465, Jul 28 '21 at 10:44
Let us [continue this discussion in chat](https://chat.stackoverflow.com/rooms/235412/discussion-between-jtlz2-and-alex3465). — jtlz2, Jul 29 '21 at 10:02

jtlz2 · Answer 1 · 2021-07-28T11:03:52.417

Thanks for posting your sample data.

Start by taking the Fourier Transform of each of the four columns in turn. arr is your data above.

import numpy as np
import matplotlib.pyplot as plt

t=np.arange(0, arr.shape[0])
plt.figure()
for icol,col in enumerate(arr.T):
    sigFFT = np.fft.fft(col) / t.shape[0]
    freq = np.fft.fftfreq(t.shape[0], d=1)
    plt.plot(freq,sigFFT)

(Huge apologies for no labels etc.)

You can see the PSF (broad features). Fit the envelope to get the PSFs. What shape PSF are you expecting? Try a sinc or some such.

How to calculate point spread function (PSF) for signal data?

1 Answers1