What type of (probably syntactic) mistake am I making when using a generic function on an array for plotting?

Question

I am trying to plot a geodesic on a 3D surface (tractrix) with Matlab. This worked for me in the past when I didn't need to parametrize the surface (see here). However, the tractrix called for parameterization, chain rule differentiation, and collection of u,v,x,y and f(x,y) values.

After many mistakes I think that I'm getting the right values for x = f1(u,v) and y = f2(u,v) describing a spiral right at the base of the surface:

What I can't understand is why the z value or height of the 3D plot of the curve is consistently zero, when I'm applying the same mathematical formula that allowed me to plot the surface in the first place, ie. f = @(x,y) a.* (y - tanh(y)) .

Here is the code, which runs without any errors on Octave. I'm typing a special note in upper case on the crucial calls. Also note that I have restricted the number of geodesic lines to 1 to decrease the execution time.

a = 0.3;

u = 0:0.1:(2 * pi);
v = 0:0.1:5;

[X,Y] = meshgrid(u,v);
% NOTE THAT THESE FORMULAS RESULT IN A SUCCESSFUL PLOT OF THE SURFACE:
x = a.* cos(X) ./ cosh(Y);
y = a.* sin(X) ./ cosh(Y);
z = a.* (Y - tanh(Y));

h = surf(x,y,z);
zlim([0, 1.2]);
set(h,'edgecolor','none')
colormap summer
hold on

% THESE ARE THE GENERIC FUNCTIONS (f) WHICH DON'T SEEM TO WORK AT THE END: 
f  = @(x,y) a.* (y - tanh(y)); 
f1 = @(u,v) a.* cos(u) ./ cosh(v);
f2 = @(u,v) a.* sin(u) ./ cosh(v);

dfdu = @(u,v) ((f(f1(u,v)+eps, f2(u,v)) - f(f1(u,v) - eps, f2(u,v)))/(2 * eps) .*
                       (f1(u+eps,v)-f1(u-eps,v))/(2*eps) +
                       (f(f1(u,v), f2(u,v)+eps) - f(f1(u,v), f2(u,v)-eps))/(2 * eps) .*
                       (f2(u+eps,v)-f2(u-eps,v))/(2*eps));

dfdv = @(u,v) ((f(f1(u,v)+eps, f2(u,v)) - f(f1(u,v) - eps, f2(u,v)))/(2 * eps) .*
                       (f1(u,v+eps)-f1(u,v-eps))/(2*eps) +
                       (f(f1(u,v), f2(u,v)+eps) - f(f1(u,v), f2(u,v)-eps))/(2 * eps) .*
                       (f2(u,v+eps)-f2(u,v-eps))/(2*eps));

 
% Normal vector to the surface:
N = @(u,v) [- dfdu(u,v), - dfdv(u,v), 1]; % Normal vec to surface @ any pt.

% Some colors to draw the lines:
C = {'k','r','g','y','m','c'};

for s = 1:1     % No. of lines to be plotted.
  
% Starting points:
u0 = [0, u(length(u))];   
v0 = [0, v(length(v))]; 
du0 = 0.001; 
dv0 = 0.001;  
   
step_size = 0.00005; % Will determine the progression rate from pt to pt.
eta =  step_size / sqrt(du0^2 + dv0^2); % Normalization.
eps = 0.0001;          % Epsilon
max_num_iter = 100000; % Number of dots in each line.
 
 
% Semi-empty vectors to collect results:
U = [[u0(s), u0(s) + eta*du0], zeros(1,max_num_iter - 2)]; 
V = [[v0(s), v0(s) + eta*dv0], zeros(1,max_num_iter - 2)]; 


for i = 2:(max_num_iter - 1)  % Creating the geodesic:
 
  ut = U(i); 
  vt = V(i);
  xt = f1(ut,vt);
  yt = f2(ut,vt);
  ft = f(xt,yt);

  utm1 = U(i - 1);  
  vtm1 = V(i - 1);
  xtm1 = f1(utm1,vtm1);
  ytm1 = f2(utm1,vtm1);
  ftm1 = f(xtm1,ytm1);

  usymp = ut + (ut - utm1);
  vsymp = vt + (vt - vtm1);
  xsymp = f1(usymp,vsymp);
  ysymp = f2(usymp,vsymp);
  fsymp = ft + (ft - ftm1);

  df = fsymp - f(xsymp,ysymp); % Is the surface changing? How much?
  n = N(ut,vt);                % Normal vector at point t
  gamma = df * n(3);           % Scalar x change f x z value of N

  xtp1 = xsymp - gamma * n(1); % Gamma to modulate incre. x & y.
  ytp1 = ysymp - gamma * n(2);

  U(i + 1) = usymp - gamma * n(1);;
  V(i + 1) = vsymp - gamma * n(2);;
 
 end

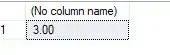
 % THE PROBLEM! f(f1(U,V),f2(U,V)) below YIELDS ALL ZEROS!!! The expected values are between 0 and 1.2.
 P = [f1(U,V); f2(U,V); f(f1(U,V),f2(U,V))]; % Compiling results into a matrix.

    units = 35; % Determines speed (smaller, faster)
    packet = floor(size(P,2)/units);
    P = P(:,1: packet * units);


  for k = 1:packet:(packet * units)
        hold on

        plot3(P(1, k:(k+packet-1)), P(2,(k:(k+packet-1))), P(3,(k:(k+packet-1))), 
            '.', 'MarkerSize', 5,'color',C{s})
        drawnow
  end
  end

The surface you plot is for `x=f1(X,Y)`, `y=f2(X,Y)` and `z=f(X,Y)`. So when drawing the line, I'd expect `f(U,V)`, not `f(f1(U,V),f2(U,V))`. — Cris Luengo, Aug 27 '21 at 17:07
@CrisLuengo I'll run it now with your changes, but in the input for `z=f(X,Y)`, for example, the `X` is actually `X=f1(U,V).` And the `Y = f2(u,v)`. — Antoni Parellada, Aug 27 '21 at 17:14
That is not what you compute at the top of your file, when you draw the surface plot. You have `z = a.* (Y - tanh(Y));`, not `z = a.* (y - tanh(y));` — Cris Luengo, Aug 27 '21 at 17:17
@CrisLuengo You are right!!!! Thanks a million! I was totally stuck, and would have spent who know how many hour staring at this thinking it was the syntax! Do you care to write a formal answer; o/w I will giving you credit. — Antoni Parellada, Aug 27 '21 at 17:19
Feel free to write the answer yourself. I don't know on which side the error actually is, I only noticed the discrepancy. — Cris Luengo, Aug 27 '21 at 17:22

Antoni Parellada · Answer 1 · 2021-08-28T23:21:52.667

The answer is to Cris Luengo's credit, who noticed that the upper-case assigned to the variable Y, used for the calculation of the height of the curve z, was indeed in the parametrization space u,v as intended, and not in the manifold x,y! I don't use Matlab/Octave other than for occasional simulations, and I was trying every other syntactical permutation I could think of without realizing that f fed directly from v (as intended). I changed now the names of the different variables to make it cleaner.

Here is the revised code:

a = 0.3;

u = 0:0.1:(3 * pi);
v = 0:0.1:5;

[U,V] = meshgrid(u,v);

x = a.* cos(U) ./ cosh(V);
y = a.* sin(U) ./ cosh(V);
z = a.* (V - tanh(V));

h = surf(x,y,z);
zlim([0, 1.2]);
set(h,'edgecolor','none')
colormap summer

hold on
 
f = @(x,y) a.* (y - tanh(y)); 
f1 = @(u,v) a.* cos(u) ./ cosh(v);
f2 = @(u,v) a.* sin(u) ./ cosh(v);

dfdu = @(u,v) ((f(f1(u,v)+eps, f2(u,v)) - f(f1(u,v) - eps, f2(u,v)))/(2 * eps) .*
                       (f1(u+eps,v)-f1(u-eps,v))/(2*eps) +
                       (f(f1(u,v), f2(u,v)+eps) - f(f1(u,v), f2(u,v)-eps))/(2 * eps) .*
                       (f2(u+eps,v)-f2(u-eps,v))/(2*eps));

dfdv = @(u,v) ((f(f1(u,v)+eps, f2(u,v)) - f(f1(u,v) - eps, f2(u,v)))/(2 * eps) .*
                       (f1(u,v+eps)-f1(u,v-eps))/(2*eps) +
                       (f(f1(u,v), f2(u,v)+eps) - f(f1(u,v), f2(u,v)-eps))/(2 * eps) .*
                       (f2(u,v+eps)-f2(u,v-eps))/(2*eps));

 
% Normal vector to the surface:
N = @(u,v) [- dfdu(u,v), - dfdv(u,v), 1]; % Normal vec to surface @ any pt.

% Some colors to draw the lines:
C = {'y','r','k','m','w',[0.8 0.8 1]}; % Color scheme

for s = 1:6     % No. of lines to be plotted.
  
% Starting points:
u0 =  [0,   -pi/2, 2*pi, 4*pi/3, pi/4, pi];   
v0 =  [0,   0,  0,  0,  0, 0]; 
du0 = [0,   -0.0001, 0.001, - 0.001, 0.001, -0.01]; 
dv0 = [0.1, 0.01,  0.001,   0.001, 0.0005, 0.01];  
   
step_size = 0.00005; % Will determine the progression rate from pt to pt.
eta =  step_size / sqrt(du0(s)^2 + dv0(s)^2); % Normalization.
eps = 0.0001;          % Epsilon
max_num_iter = 180000; % Number of dots in each line.
 
 
% Semi-empty vectors to collect results:
Uc = [[u0(s), u0(s) + eta*du0(s)], zeros(1,max_num_iter - 2)]; 
Vc = [[v0(s), v0(s) + eta*dv0(s)], zeros(1,max_num_iter - 2)]; 


for i = 2:(max_num_iter - 1)  % Creating the geodesic:
 
  ut = Uc(i); 
  vt = Vc(i);
  xt = f1(ut,vt);
  yt = f2(ut,vt);
  ft = f(xt,yt);

  utm1 = Uc(i - 1);  
  vtm1 = Vc(i - 1);
  xtm1 = f1(utm1,vtm1);
  ytm1 = f2(utm1,vtm1);
  ftm1 = f(xtm1,ytm1);

  usymp = ut + (ut - utm1);
  vsymp = vt + (vt - vtm1);
  xsymp = f1(usymp,vsymp);
  ysymp = f2(usymp,vsymp);
  fsymp = ft + (ft - ftm1);

  df = fsymp - f(xsymp,ysymp); % Is the surface changing? How much?
  n = N(ut,vt);                % Normal vector at point t
  gamma = df * n(3);           % Scalar x change f x z value of N

  xtp1 = xsymp - gamma * n(1); % Gamma to modulate incre. x & y.
  ytp1 = ysymp - gamma * n(2);

  Uc(i + 1) = usymp - gamma * n(1);;
  Vc(i + 1) = vsymp - gamma * n(2);;
 
 end
 
 x = f1(Uc,Vc);
 y = f2(Uc,Vc);

 P = [x; y; f(Uc,Vc)]; % Compiling results into a matrix.

    units = 35; % Determines speed (smaller, faster)
    packet = floor(size(P,2)/units);
    P = P(:,1: packet * units);


  for k = 1:packet:(packet * units)
        hold on

        plot3(P(1, k:(k+packet-1)), P(2,(k:(k+packet-1))), P(3,(k:(k+packet-1))), 
            '.', 'MarkerSize', 5,'color',C{s})
        drawnow
  end
  end

What type of (probably syntactic) mistake am I making when using a generic function on an array for plotting?

1 Answers1