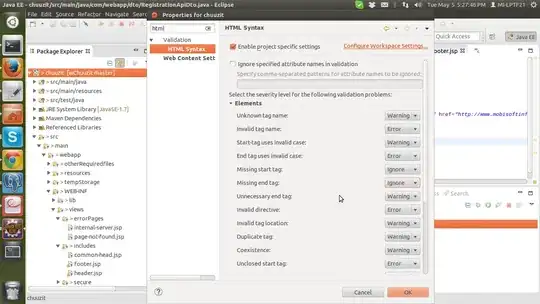
I am trying generate a vector plot of the gradient of a 2D gaussian function in python, that should look like this:
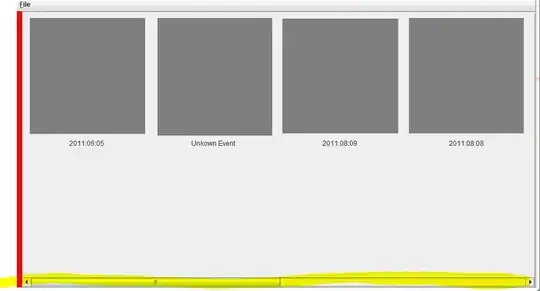
However, the code I have adapted produces the following. (The gradient of a 2D gaussian should not produce arrows pointing in the directions shown in this plot):
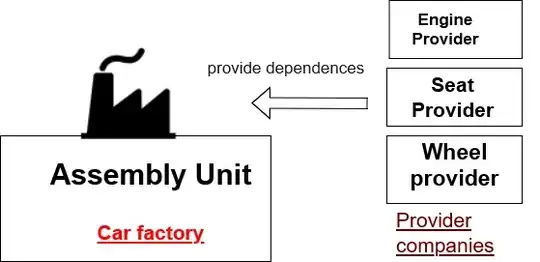
From a 2D gaussian here:
Can someone help explain what is at fault with the following code? The main parts are from (a) 2D gaussian, (b) splitting gradient array into x and y components and (c) vector quiver plot with arrows.
import numpy as np
from matplotlib import pyplot as plt
# define normalized 2D gaussian
def gaus2d(x=0, y=0, mx=0, my=0, sx=1, sy=1):
return 1. / (2. * np.pi * sx * sy) * np.exp(-((x - mx)**2. / (2. * sx**2.) + (y - my)**2. / (2. * sy**2.)))
x = np.linspace(-5, 5)
y = np.linspace(-5, 5)
x, y = np.meshgrid(x, y) # get 2D variables instead of 1D
z = gaus2d(x, y)
gauss_grad = np.gradient(z) # calculating array of gaussian gradient
nx, ny = 50, 50
x1 = range(nx)
y1 = range(ny)
U = gauss_grad[0] # x component of gaussian gradient
V = gauss_grad[1] # y component of gaussian gradient
print(" Value of U: ", U)
print(" Value of V: ", V)
X1, Y1 = np.meshgrid(x1, y1)
fig, hf = plt.subplots(figsize=(10,10)) # setting up quiver plot
hf.set_title("Example - gradient of gaussian- every 2nd arrow")
Q = hf.quiver(X1[::2, ::2], Y1[::2, ::2], U[::2, ::2], V[::2, ::2], units='width',
pivot='mid', scale=0.1, headwidth=5)
qk = hf.quiverkey(Q, 0.9, 0.9, 0.1, r'$2d \ vector \ plot$', labelpos='E',
coordinates='figure')
hf.scatter(X1[::2, ::2], Y1[::2, ::2], color='c', s=0)
plt.show()
#plt.contourf(x, y, z, cmap='Blues')
#plt.colorbar()
#plt.show()