Genetic Algorithm Population Individual as Array

Question

I don't have much experience using Genetic Algorithms, so I would like to ask the community for some useful comments. I want to apologize for my terminology errors. Please, correct me if it's needed.

The problem I want to optimize is optimal power flow in an islanded microgrid. In the simple microgrid we have 2 diesel generators (DG), 1 PV array, 1 Energy Storage System (ESS) and Load. Let's assume we know Load and PV array output power values for next periods.

So, the objective function should be minimized is OPEX as sum of every microgrid component operational cost at each moment t in period T:

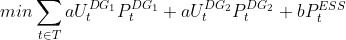
where a, b are some operational cost coefficients, 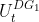is diesel generator binary (0/1 or ON/OFF) status variable and P is output power of the microgrid component at the time t.

And here are some of constraints (the real problem is hardly and nonlinearly constrained so I wrote down only three of constraints):

1. Power balance

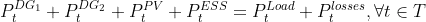
2. ESS' Maximum depth of disharge

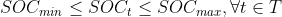
3. Diesel gensets power limit

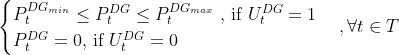
So, it's mixed integer problem with nonlinear constraints. I tried to adapt the problem for solving it using Genetic Algorithm. I used pymoo Python library for multiobjective optimization with NSGA2 algorithm. Let's consider 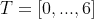and for this T we have some Load and PV power data:

from pymoo.model.problem import FunctionalProblem
from pymoo.factory import get_sampling, get_crossover, get_mutation
from pymoo.operators.mixed_variable_operator import MixedVariableSampling, MixedVariableMutation, MixedVariableCrossover
from pymoo.algorithms.nsga2 import NSGA2
from pymoo.factory import get_sampling, get_crossover, get_mutation, get_termination
from pymoo.optimize import minimize

PV = np.array([10, 19.8, 16, 25, 7.8, 42.8, 10]) #PV inverter output power, kW
Load = np.array([100, 108, 150, 150, 90, 16, 170]) #Load, kW

balance_eps = 0.001 #equality constraint relaxing coefficient

DG1_pmin = 0.3 #DG1 min power
DG2_pmin = 0.3 #DG2 min power
P_dg1 = 75 #DG1 rated power, kW
P_dg2 = 75 #DG1 rated power, kW

P_PV_inv = 50 #PV inverter rated power, kW

P_ESS_inv = 30 #ESS bidirectional inverter absolute rated discharge/charge power, kW

ESS_c = 100 #ESS capacity, kWh

SOC_min = 30
SOC_max = 100
    
objs = [lambda x: x[0]*x[2]*200 + x[1]*x[3]*200 + x[4]*0.002 #objective function]

constr_eq = [lambda x: ((Load[t] - x[0]*x[2] - x[1]*x[3] - x[4] - PV[t] )**2)]

constr_ieq = [lambda x: -SOC_t + 100*x[4]/ESS_c + SOC_min,
    lambda x: SOC_t - 100*x[4]/ESS_c - SOC_max]

problem = FunctionalProblem(n_var=n_var, objs, constr_eq=constr_eq, constr_eq_eps=1e-03, constr_ieq=constr_ieq, 
          xl=np.array([0, 0, DG1_pmin*P_dg1, DG2_pmin*P_dg2, -P_ESS_inv]), xu=np.array([1, 1, P_dg1, P_dg2, P_ESS_inv]))

mask = ["int", "int", "real", "real", "real"]

sampling = MixedVariableSampling(mask, {
    "real": get_sampling("real_random"),
    "int": get_sampling("int_random")})

crossover = MixedVariableCrossover(mask, {
    "real": get_crossover("real_sbx", prob=1.0, eta=3.0),
    "int": get_crossover("int_sbx", prob=1.0, eta=3.0)})

mutation = MixedVariableMutation(mask, {
    "real": get_mutation("real_pm", eta=3.0),
    "int": get_mutation("int_pm", eta=3.0)})

algorithm = NSGA2(
    pop_size=150,
    sampling=sampling,
    crossover=crossover,
    mutation=mutation,
    eliminate_duplicates=True)

We have n_var = 5 decision variables which are being optimized: 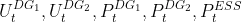. We should also have an access to the previous value of SOC. I wrote a recursive code to implement a consecutive optimization chain:

x=[]
s=[]
SOC_t = 100 #SOC at t = -1

for t in range (0, 7):

    res = minimize(
        problem,
        algorithm,
        seed=1,
        termination = get_termination("n_gen", 300),
        save_history=True, verbose=False)

    SOC_t = SOC_t - 100*res.X[4]/ESS_c

    print(res.X[:2], np.around(res.X[2:].astype(np.double), 3), np.around(SOC_t, 2))
    x.append(res.X)
    s.append(SOC_t) 

So, we have initialized populations with size 150 for every time step t and individuals in that populations looked like 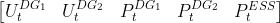. Running this code I get these optimization results found:

[1 1] [27.272 34.635 28.071] 71.93
[0 1] [28.127 58.168 30.   ] 41.93
[1 1] [50.95  71.423 11.599] 30.33
[1 1] [53.966 70.97  0.034] 30.3
[1 1] [24.636 59.236 -1.702] 32.0
[0 0] [40.831  29.184 -26.832] 58.83
[1 1] [68.299 63.148 28.572] 30.26

Even my little experience in Genetic Algorithms allows me to state, that such approach is inappropriate and unefficient.

So, here is my question (if you're still reading my post :)

Is there a way to optimize such problem using not consecutive optimization of a particular variables set at t, but defining individuals in population as arrays with size (T, n_var)?

For the problem described an individual in population may look like

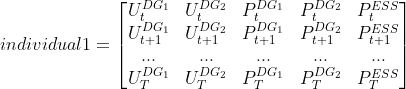
Is it possible to implement such approach? If yes, how to do it in pymoo?

Thank you very much for your time! Any comments and suggestions will be appreciated.