I have an interval, say (0, 9) and I have to generate points between them such that they are denser at the both the boundaries. I know the number of points, say n_x. alpha decides the "denseness" of the system such that points are evenly spaced if alpha = 1.
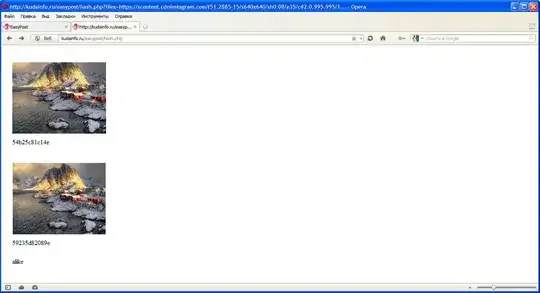
The cross product of n_x and n_y is supposed to look like this:
[
So far the closest I've been to this is by using np.geomspace, but it's only dense near the left-hand side of the domain,
In [55]: np.geomspace(1,10,15) - 1
Out[55]:
array([0. , 0.17876863, 0.38949549, 0.63789371, 0.93069773,
1.27584593, 1.6826958 , 2.16227766, 2.72759372, 3.39397056,
4.17947468, 5.1054023 , 6.19685673, 7.48342898, 9. ])
I also tried dividing the domain into two parts, (0,4), (5,10) but that did not help either (since geomspace gives more points only at the LHS of the domain).
In [29]: np.geomspace(5,10, 15)
Out[29]:
array([ 5. , 5.25378319, 5.52044757, 5.80064693, 6.09506827,
6.40443345, 6.72950096, 7.07106781, 7.42997145, 7.80709182,
8.20335356, 8.61972821, 9.05723664, 9.51695153, 10. ])
Apart from that, I am a bit confused about which mathematical function can I use to generate such an array.