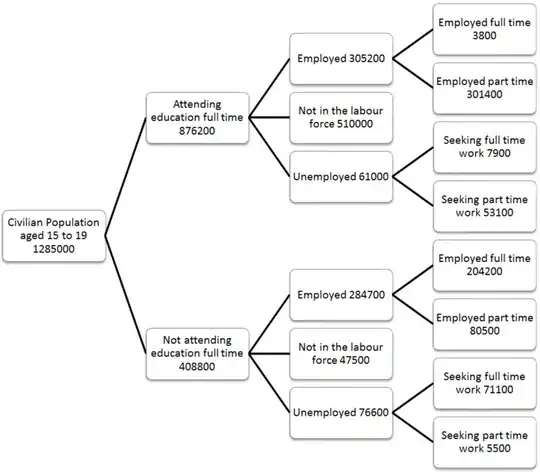
I would like to find the intersection of two graphs. It took me 674 points to plot the first graph and only 14 points to plot the second graph.
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
df = pd.read_csv("test1.csv",,skiprows=range(9),names=['A', 'B', 'C','D'])
df2 = pd.read_csv("test2.csv",skiprows=range(1),names=['X','Y'])
x1 = df['A'].tolist()
x1 = np.array(x1)
y1 = df['D'].tolist()
y1 = np.array(y1)
x2 = df2['X'].tolist()
x2 = np.array(x2)
y2 = df2['Y'].tolist()
y2 = np.array(y2)
idx = np.argwhere(np.diff(np.sign(y1 - y2))).flatten()
fig, ax = plt.subplots()
ax.plot(x1, y1, 'blue')
ax.plot(x2, y2, 'red')
plt.show()
However, I am getting this error from the code above due to the different sizes of numpy. Any ways I can solve this?
operands could not be broadcast together with shapes (674,) (14,)