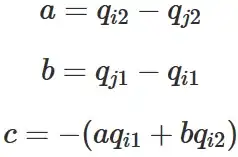2

I have been looking at how to reflect a point in a line, and found this question which seems to do the trick, giving this formula to calculate the reflected point:

Given (x,y) and a line y = ax + c we want the point (x', y') reflected on the line.

Set d:= (x + (y - c)*a)/(1 + a^2)

Then x' = 2*d - x

and y' = 2*d*a - y + 2c

However there are two problems with this implementation for my needs:

  1. My line is not described in the form y = ax + c (so I'd have to translate it, which is easy to do, but it means the process is slower).
  2. What if a is infinity ie. a vertical line?

Is there a simple way to calculate (x', y'), the reflection of point (x, y) in a line, where the line is described by the two points (x1, y1) and (x2, y2)?

Edit:

I've found a formula which does this, but it seems as though it does not work with lines that look like they have equation y = x.

Here it is in actionscript:

public static function reflect(p:Point, l:Line):Point
    {
                    // (l.sx, l.sy) = start of line
                    // (l.ex, l.ey) = end of line
        var dx:Number = l.ex - l.sx;
        var dy:Number = l.ey - l.sy;

        if ((dx == 0) && (dy == 0))
        {
            return new Point(2 * l.sx - p.x, 2 * l.sy - p.y);
        }
        else
        {
            var t:Number = ((p.x - l.sx) * dx + (p.y - l.sy) * dy) / (dx * dx + dy * dy);
            var x:Number = 2 * (l.sx + t * dx) - p.x;
            var y:Number = 2 * (l.sy + t * dy) - p.y;
            return new Point(x, y);
        }
    }

Does anyone have any idea where this formula goes wrong? I am still happy to take other solutions than the above formula - anything that'll work!

Community
  • 1
  • 1
Jack
  • 2,153
  • 5
  • 28
  • 43

3 Answers3

4

I was looking for an answer to the same question. For this paper I have derived the equation and written the code for an edge of a polygon.

Reflection of a point across an edge of a polygon

Reflection of a 2D point p0 across a line which is passing through two vertices qi, qj can be calculated as,

Equation of the reflected point

where

a, b, c

The python code is below:

def reflection_of_point(p_0, q_i, q_j):
    """Calculates reflection of a point across an edge

    Args:
        p_0 (ndarray): Inner point, (2,)
        q_i (ndarray): First vertex of the edge, (2,)
        q_j (ndarray): Second vertex of the edge, (2,)

    Returns:
        ndarray: Reflected point, (2,)
    """    

    a = q_i[1] - q_j[1]
    b = q_j[0] - q_i[0]
    c = - (a * q_i[0] + b * q_i[1])

    p_k = (np.array([[b**2 - a**2, -2 * a * b],
                     [-2 * a * b, a**2 - b**2]]) @ p_0 - 2 * c * np.array([a, b])) / (a**2 + b**2)

    return p_k
rszengin
  • 331
  • 2
  • 4
1

Find the normal vector from the point onto the line and add it twice to the point. See wikipedia for the formula.

If you express everything in vectors you won't have the problems with an infinite slope.

;; line defined by ax+by+c=0
;; normal (a b) and distance from origin -c
(defun reflect-point-on-line (a b c px py)
  (/ (+ (* a px)
    (* b py)
    c)
     (sqrt (+ (expt a 2) (expt b 2)))))
#+nil ;; y-axis to (2 1)
(reflect-point-on-line 1 0 0 2 1) ;; => 2
#+nil ;; x-axis to (4 5)
(reflect-point-on-line 0 1 0 4 5) ;; => 5
whoplisp
  • 2,508
  • 16
  • 19
  • Thanks for your reply, although I'm still a little confused... How do I calculate this normal? The normal of a line with direction vector (x, y) is (-y, x), but how do I find the distance I need to move the point in that direction? I've also found a different formula to calculate the reflected point, but this is breaking for 45 degree diagonal lines (ie with formula y=x). I've added it to my post. – Jack Aug 05 '11 at 22:28
  • See the first equation for Ref_l(v) in the Wikipedia article. – whoplisp Aug 06 '11 at 02:53
  • An important part of the solution is to understand how to calculate the distance between a point and a line: http://mathworld.wolfram.com/Point-LineDistance2-Dimensional.html. – whoplisp Aug 06 '11 at 02:59
0

If your line is 45 degrees... y = x...then your point (x1,y1) is one corner of a square, your line has two points on it that correspond to your point (x1 + distance to line, y1) and (x1, y1 plus distance to line) and the point you're looking for is the opposite corner, no?

If you find your distance, you should be able to add them to your coords and get your new point.