How can I plot a CDF in Matplotlib without binning my data?

Question

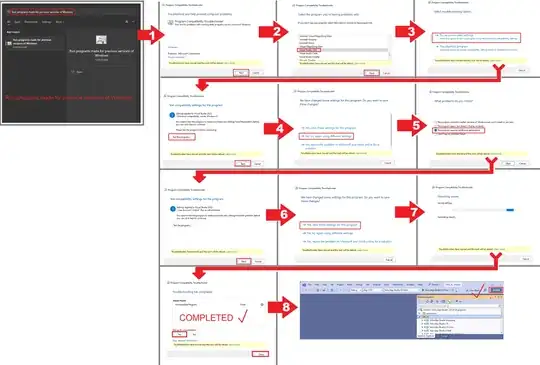
I can easily make a CDF in Matplotlib by using a cumulative histogram:

data = np.linspace(0, 100, num=10000)
plt.hist(data, cumulative=True, density=1)

And the result is this:

I can crank up the bin count to get a better approximation:

plt.hist(data, bins=50, cumulative=True, density=1)

Now the result is:

This is still not great. I know I can just make the bin count even higher, but that's a pretty unsatisfying solution for me.

Is there a way to plot a CDF that doesn't make me lose some precision? Like a binless histogram or something else?

Use [`seaborn.ecdfplot`](https://seaborn.pydata.org/generated/seaborn.ecdfplot.html): Does this help? [How to use markers with ECDF plot](https://stackoverflow.com/q/69300483/7758804) — Trenton McKinney, Oct 11 '21 at 16:43

score 1 · Answer 1 · answered Oct 11 '21 at 02:58

You're talking about the ECDF (empirical cumulative distribution function) derived from the sample, and a cumulative histogram isn't how it's typically done. What's usually done is sorting the sample, finding the unique values, and finding the proportion of the sample less than or equal to those unique values; no need to adjust bin-widths.

The ECDF has discontinuous jumps at every unique value, so you'd want 2 values for each jump for plotting's sake. The following code will give you the x and y to plot an ECDF:

def ecdf4plot(seq, assumeSorted = False):
    """
    In:
    seq - sorted-able object containing values
    assumeSorted - specifies whether seq is sorted or not
    Out:
    0. values of support at both points of jump discontinuities
    1. values of ECDF at both points of jump discontinuities
       ECDF's true value at a jump discontinuity is the higher one    """
    if not assumeSorted:
        seq = sorted(seq)
    prev = seq[0]
    n = len(seq)
    support = [prev]
    ECDF = [0.]
    for i in range(1, n):
        seqi = seq[i]
        if seqi != prev:
            preP = i/n
            support.append(prev)
            ECDF.append(preP)
            support.append(seqi)
            ECDF.append(preP)
            prev = seqi
    support.append(prev)
    ECDF.append(1.)
    return support, ECDF

# example usage
import numpy as np
from matplotlib import pyplot as plt

plt.plot(*ecdf4plot(np.random.randn(100)))

How can I plot a CDF in Matplotlib without binning my data?

1 Answers1