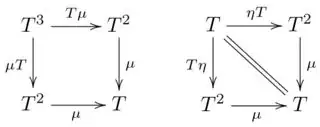
The laws for monoids in the category of endofunctors are:
And the Haskell monad laws are:
Left identity: return a >>= k = k a
Right identity: m >>= return = m
Associativity: m >>= (\x -> k x >>= h) = (m >>= k) >>= h
I'm assuming the latter is derived from the former, but how so? The diagrams basically say
join (join x) = join (fmap join x)
join (return x) = x
join (fmap return x) = x
How are these equivalent to the Haskell monad laws?