How do you draw a partition plane from a classification algorithm in a 3D plot in R

Question

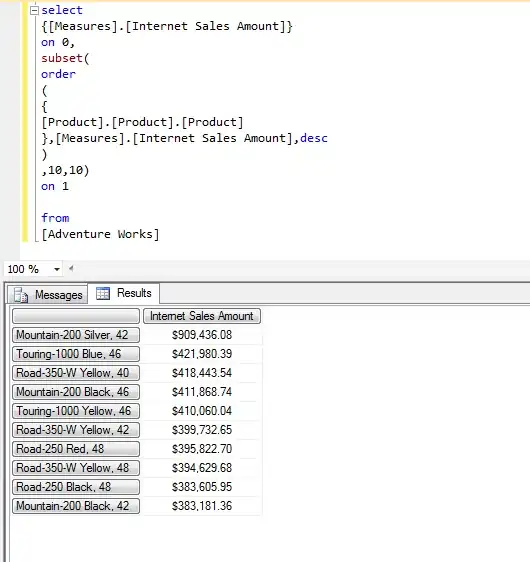
I'm trying to draw a partition border from a classification algorithm in a 3D plot in R (using plot3D). It's a relatively simple task if we only have two predictors, requiring only two axes to draw (e.g. using the partimat function). I haven't yet found a satisfactory way to draw a three predictor-based classification partition in 3D space.

To visualise the problem, let's start by building a partition for just two axes using a Linear Discriminant Analysis (LDA) classification algorithm on the iris dataset:

# Load packages and subset the iris dataset:
library(klaR)

data = droplevels(iris[iris$Species != 'virginica', ])

partimat(Species ~ Sepal.Length + Sepal.Width, data, 
         method = 'lda')

We get a 2D plot with a clearly defined partition between the two species:

However, partimat can only handle two predictors at a time (see ?partimat). Let's now look at the 3D problem:

library(plot3D)
    
# Plot the raw data:
points3D(data$Sepal.Length, data$Sepal.Width, data$Petal.Length,
             colkey = F,
             pch = 16, cex = 2,
             theta = 30, phi = 30, 
             ticktype = 'detailed',
             col = data$Species)

I want to draw a plane separating the two data classes based on a classification algorithm like LDA. Drawing inspiration from Roman Luštrik's example, here's my poor attempt at defining the partition between three predictors. Essentially, I've built a LDA model with three predictors, then predicted the species (setosa or versicolor) onto multiple points between the max. and min. values of all three predictors. When plotted on a 3D plot, this generates a point cloud, coloured differently to represent the 3D space where either iris species should appear based on the three predictors:

# Build a classification model with three predictors:
m = lda(Species ~ Sepal.Length + Sepal.Width + Petal.Length, data)

# Predict 'Species' for the full range of each plant metric: 
np = 50

nx = seq(from = min(data[, 1]), to = max(data[, 1]), length.out = np)
ny = seq(from = min(data[, 2]), to = max(data[, 2]), length.out = np)
nz = seq(from = min(data[, 3]), to = max(data[, 3]), length.out = np)
nd = expand.grid(Sepal.Length = nx, Sepal.Width = ny, Petal.Length = nz)

p    = as.numeric(predict(m, newdata = nd)$class)
part = cbind(nd, Partition = p)

# Plot the partition and add the data points:  
scatter3D(part$Sepal.Length, part$Sepal.Width, part$Petal.Length, 
          colvar = part$Partition, 
          colkey = F,
          alpha = 0.5,
          pch = 16, cex = 0.3, 
          theta = 30, phi = 30, 
          ticktype = 'detailed',
          plot = F)
points3D(data$Sepal.Length, data$Sepal.Width, data$Petal.Length,
         colkey = F,
         pch = 16, cex = 2,
         theta = 30, phi = 30, 
         ticktype = 'detailed',
         col = data$Species,
         add = T)

I've also added the data points. You can make out the partition as the fuzzy intersection between blue and red in the pointcloud:

This isn't an ideal solution, as it's difficult to see the data points hidden amongst the point cloud. The point cloud is also a little bit distracting. Maybe some clever plotting of the points with transparency would improve things, but I suspect a much nicer solution would be to draw a plane (similar to a regression plane) at the intersect between species classes (i.e. where the blue and red dots meet). Note, I ultimately wish to use different classifiers (e.g. Random Forest) just in case there's a solution out there limited only to LDA or similar.

Many thanks in advance for any solutions or advice.

Allan Cameron · Accepted Answer · 2021-10-29T19:37:44.220

You can use the coefficients from the lda model to generate a plane separating the discriminant volumes. Effectively, the plane is the set of points in the 3D space where the sum of the (x, y, z) co-ordinates multiplied by their respective coefficients from the model is equal to the model's threshold (i.e. the plane where the model can't discriminate one group from the other).

We can do this by creating a 10 x 10 grid of equally spaced values along the x and y axes and calculating the z value that gives us the threshold value based on the model:

threshold <-  sum(coef(m) * data[1, 1:3]) - predict(m)$x[1] 

Sepal_Lengths <- seq(min(data$Sepal.Length), max(data$Sepal.Length), length.out = 10)
Sepal_Widths  <- seq(min(data$Sepal.Width), max(data$Sepal.Width), length.out = 10)
Petal_Lengths <- outer(Sepal_Lengths, Sepal_Widths, function(x, y) {
                  (threshold - x * coef(m)[1] - y * coef(m)[2]) / coef(m)[3]})

So now when we draw our points:

points3D(data$Sepal.Length, data$Sepal.Width, data$Petal.Length,
         colkey = F,
         pch = 16, cex = 2,
         theta = 30, phi = 30, 
         ticktype = 'detailed',
         col = data$Species)

Adding the plane is as easy as:

persp3D(x = Sepal_Lengths, 
        y = Sepal_Widths, 
        z = Petal_Lengths, 
        col = "gold", add = TRUE, alpha = 0.5)

How do you draw a partition plane from a classification algorithm in a 3D plot in R

1 Answers1