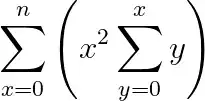Efficient summation in Python

Question

I am trying to efficiently compute a summation of a summation in Python:

WolframAlpha is able to compute it too a high n value: sum of sum.

I have two approaches: a for loop method and an np.sum method. I thought the np.sum approach would be faster. However, they are the same until a large n, after which the np.sum has overflow errors and gives the wrong result.

I am trying to find the fastest way to compute this sum.

import numpy as np
import time

def summation(start,end,func):
    sum=0
    for i in range(start,end+1):
        sum+=func(i)
    return sum

def x(y):
    return y

def x2(y):
    return y**2

def mysum(y):
    return x2(y)*summation(0, y, x)

n=100

# method #1
start=time.time()
summation(0,n,mysum)
print('Slow method:',time.time()-start)

# method #2
start=time.time()
w=np.arange(0,n+1)
(w**2*np.cumsum(w)).sum()
print('Fast method:',time.time()-start)

Answer 1

Here's a very fast way:

result = ((((12 * n + 45) * n + 50) * n + 15) * n - 2) * n // 120

How I got there:

1. Rewrite the inner sum as the well-known x*(x+1)//2. So the whole thing becomes sum(x**2 * x*(x+1)//2 for x in range(n+1)).
2. Rewrite to sum(x**4 + x**3 for x in range(n+1)) // 2.
3. Look up formulas for sum(x**4) and sum(x**3).
4. Simplify the resulting mess to (12*n**5 + 45*n**4 + 50*n**3 + 15*n**2 - 2*n) // 120.
5. Horner it.

Another way to derive it if after steps 1. and 2. you know it's a polynomial of degree 5:

3. Compute six values with a naive implementation.
4. Compute the polynomial from the six equations with six unknowns (the polynomial coefficients). I did it similarly to this, but my matrix A is left-right mirrored compared to that, and I called my y-vector b.

Code:

from fractions import Fraction
import math
from functools import reduce

def naive(n):
    return sum(x**2 * sum(range(x+1)) for x in range(n+1))

def lcm(ints):
    return reduce(lambda r, i: r * i // math.gcd(r, i), ints)

def polynomial(xys):
    xs, ys = zip(*xys)
    n = len(xs)
    A = [[Fraction(x**i) for i in range(n)] for x in xs]
    b = list(ys)
    for _ in range(2):
        for i0 in range(n):
            for i in range(i0 + 1, n):
                f = A[i][i0] / A[i0][i0]
                for j in range(i0, n):
                    A[i][j] -= f * A[i0][j]
                b[i] -= f * b[i0]
        A = [row[::-1] for row in A[::-1]]
        b.reverse()
    coeffs = [b[i] / A[i][i] for i in range(n)]
    denominator = lcm(c.denominator for c in coeffs)
    coeffs = [int(c * denominator) for c in coeffs]
    horner = str(coeffs[-1])
    for c in coeffs[-2::-1]:
        horner += ' * n'
        if c:
            horner = f"({horner} {'+' if c > 0 else '-'} {abs(c)})"
    return f'{horner} // {denominator}'

print(polynomial((x, naive(x)) for x in range(6)))

Output (Try it online!):

((((12 * n + 45) * n + 50) * n + 15) * n - 2) * n // 120

Answer 2

(fastest methods, 3 and 4, are at the end)

In a fast NumPy method you need to specify dtype=np.object so that NumPy does not convert Python int to its own dtypes (np.int64 or others). It will now give you correct results (checked it up to N=100000).

# method #2
start=time.time()
w=np.arange(0, n+1, dtype=np.object)
result2 = (w**2*np.cumsum(w)).sum()
print('Fast method:', time.time()-start)

Your fast solution is significantly faster than the slow one. Yes, for large N's, but already at N=100 it is like 8 times faster:

start=time.time()
for i in range(100):
    result1 = summation(0, n, mysum)
print('Slow method:', time.time()-start)

# method #2
start=time.time()
for i in range(100):
    w=np.arange(0, n+1, dtype=np.object)
    result2 = (w**2*np.cumsum(w)).sum()
print('Fast method:', time.time()-start)

Slow method: 0.06906533241271973
Fast method: 0.008007287979125977

EDIT: Even faster method (by KellyBundy, the Pumpkin) is by using pure python. Turns out NumPy has no advantage here, because it has no vectorized code for np.objects.

# method #3
import itertools
start=time.time()
for i in range(100):
    result3 = sum(x*x * ysum for x, ysum in enumerate(itertools.accumulate(range(n+1))))
print('Faster, pure python:', (time.time()-start))

Faster, pure python: 0.0009944438934326172

EDIT2: Forss noticed that numpy fast method can be optimized by using x*x instead of x**2. For N > 200 it is faster than pure Python method. For N < 200 it is slower than pure Python method (the exact value of boundary may depend on machine, on mine it was 200, its best to check it yourself):

# method #4
start=time.time()
for i in range(100):
    w = np.arange(0, n+1, dtype=np.object)
    result2 = (w*w*np.cumsum(w)).sum()
print('Fast method x*x:', time.time()-start)

Answer 3

Comparing Python with WolframAlpha like that is unfair, since Wolfram will simplify the equation before computing.

Fortunately, the Python ecosystem knows no limits, so you can use SymPy:

from sympy import summation
from sympy import symbols

n, x, y = symbols("n,x,y")
eq = summation(x ** 2 * summation(y, (y, 0, x)), (x, 0, n))
eq.evalf(subs={"n": 1000})

It will compute the expected result almost instantly: 100375416791650. This is because SymPy simplifies the equation for you, just like Wolfram does. See the value of eq:

@Kelly Bundy's answer is awesome, but if you are like me and use a calculator to compute 2 + 2, then you will love SymPy ❤. As you can see, it gets you to the same results with just 3 lines of code and is a solution that would also work for other more complex cases.

Answer 4

All the answers uses math to simplify or implement the loop in python trying to be cpu optimal, but they are not memory optimal.

Here a naive implementation without using any math simplification which is memory efficient

def function5():
    inner_sum = float()
    result = float()

    for x in range(0, n + 1):
        inner_sum += x
        result += x ** 2 * inner_sum
        
    return result

It is quite slow with respect to the other solutions by dankal444:

method 2   | 31 µs ± 2.06 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
method 3   | 116 µs ± 538 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
method 4   | 91 µs ± 356 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
function 5 | 217 µs ± 1.14 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

by the way if you jit the function with numba (there may be better options):

from numba import jit
function5 = jit(nopython=True)(function5)

you get

59.8 ns ± 0.209 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)

Answer 5

In a comment, you mention that it's really f(x) and g(y) instead of x² and y. If you're only needing an approximation to that sum, you can pretend the sums are midpoint Riemann sums, so that your sum is approximated by the double integral ∫_-.5^n+.5 f(x) ∫_-.5^x+.5 g(y) dy dx.

With your original f(x)=x² and g(y)=y, this simplifies to n⁵/10+3n⁴/8+n³/2+5n²/16+3n/32+1/160, which differs from the correct result by n³/12+3n²/16+53n/480+1/160.

Based on this, I suspect that (actual-integral)/actual would be max(f'',g'')*O(n^-2), but I wasn't able to prove it.