Sigmoid curve detection

Question

I have tabular data-set representing curves, each curve is represented by 42 values(data points), the goal is to filter out curves that do not follow Sigmoid function.

Technique applied

Sigmoid Curve Fitting
Calculate goodness of curve

Curve fitting source

from scipy.optimize import curve_fit
def sigmoid(x, L=max(y), x0=21, k=0.6, b=5):
    y = L / (1 + np.exp(-k*(x-x0)))+b
    return (y)

p0 = [max(y), np.median(x),1,min(y)] 

popt, pcov = curve_fit(sigmoid, x, y, p0, method='dogbox',  maxfev=10000)

Plotting

yd = sigmoid(x, *popt)
plt.plot(x, y, 'o', label='data')
plt.plot(x,yd, label='fit')
plt.legend(loc='best')
plt.show()

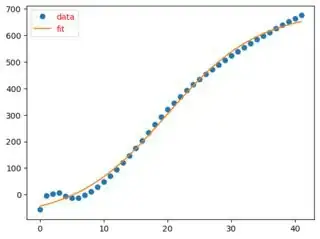
r2_score(y, yd) = 0.99

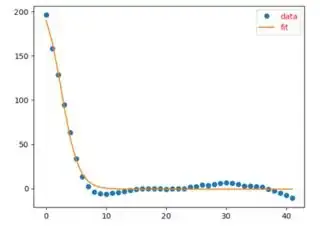
but even when curve is not sigmoid, cuve fit very well andI get fitness of curve r2_score(y, yd) = 0.98

Example data

    **Sigmoid**
        [154.02811505496447,
         146.39766673379745,
         130.55841841263054,
         105.90461009146338,
         66.8461297702961,
         22.543803049129565,
         -13.688227352037302,
         -31.754967769204086,
         -36.574590925571556,
         -34.31173263297842,
         -27.98295459843348,
         -17.624496325705877,
         -2.2469180569519267,
         20.740420258644008,
         54.053534582814336,
         104.15375611806758,
         180.67655429725164,
         299.0412892474392,
         473.8589268806131,
         712.1355324045853,
         1010.3945120433141,
         1353.3417600831544,
         1722.423136626168,
         2095.8689925500385,
         2453.614570050715,
         2779.492987742925,
         3064.6579177888016,
         3304.9067183437182,
         3500.629595471177,
         3654.4640620149517,
         3773.8156617564973,
         3866.2930060208614,
         3937.098925829344,
         3990.995709651212,
         4032.976381384583,
         4066.19200350293,
         4094.2713932805746,
         4117.570526667072,
         4137.0863623072,
         4154.089487119825,
         4169.671081872018,
         4185.233572233441]
     Non sigmoid
[489.2834973631293,
 361.00794898560935,
 263.98040060808944,
 176.09045223057,
 110.87762385304995,
 63.42773947552996,
 42.065867898009856,
 29.47418768048965,
 23.254148294970037,
 17.262475347849886,
 13.390803854810201,
 5.18880594026632,
 -4.0552569677629435,
 -9.77379815878885,
 -15.39564800511198,
 -17.0930552390937,
 -22.386235681666676,
 -24.01368224348971,
 -27.6271366708811,
 -28.704645895235444,
 -26.672167652096505,
 -20.310502874851863,
 -17.661003297287152,
 -15.088099452837014,
 -15.872947794945503,
 -8.34466572098927,
 -1.6253080011324528,
 6.594890931118698,
 10.953473235028014,
 14.039900455748466,
 17.299573334162687,
 16.739464327477435,
 16.650048075311133,
 13.090813997028818,
 12.731754904427362,
 12.118767243738603,
 12.095028866568555,
 11.33835463248488,
 5.952943083721948,
 -0.7048030993591965,
 -9.088792078874576,
 -15.823553268803153]

Related work

The thing is, the second curve you plotted does fit very well to the tail end of a sigma curve reflected in the y-axis. The maths is behaving exactly as expected. You may need to add an additional constraint on k (to be non-negative, off the top of my head), or consider other heuristics like looking at the gradient at the two bounds of your range. — butterflyknife, Nov 16 '21 at 11:24

score 1 · Accepted Answer · answered Nov 16 '21 at 12:36

The problem is that you are using unbounded parameters. For example, if you allow L to be negative, you can fit a monotonically decreasing dataset with your function.

If I add simple non-negativity bounds to your fit, I get:

def sigmoid(x, L=max(y), x0=21, k=0.6, b=5):
    y = L / (1 + np.exp(-k*(x-x0)))+b
    return (y)

p0 = [max(y), np.median(x), 1, 0] 

popt, pcov = curve_fit(sigmoid, x, y, p0, method='dogbox',  maxfev=10000, bounds=(0, np.inf))

Sigmoid:

Non sigmoid:

You can play with the bounds to better restrict the fitting to your allowable range of shapes.

Sigmoid curve detection

1 Answers1