11

I would like to improve the performance of hashing large files, say for example in the tens of gigabytes in size.

Normally, you sequentially hash the bytes of the files using a hash function (say, for example SHA-256, although I will most likely use Skein, so hashing will be slower when compared to the time it takes to read the file from a [fast] SSD). Let's call this Method 1.

The idea is to hash multiple 1 MB blocks of the file in parallel on 8 CPUs and then hash the concatenated hashes into a single final hash. Let's call this Method 2.

A picture depicting this method follows:

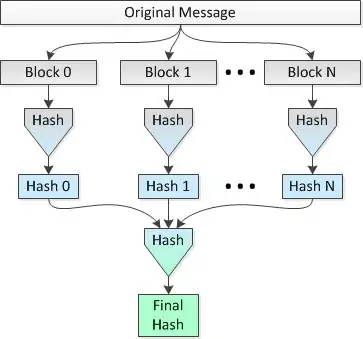
enter image description here

I would like to know if this idea is sound and how much "security" is lost (in terms of collisions being more probable) vs doing a single hash over the span of the entire file.

For example:

Let's use the SHA-256 variant of SHA-2 and set the file size to 2^34=34,359,738,368 bytes. Therefore, using a simple single pass (Method 1), I would get a 256-bit hash for the entire file.

Compare this with:

Using the parallel hashing (i.e., Method 2), I would break the file into 32,768 blocks of 1 MB, hash those blocks using SHA-256 into 32,768 hashes of 256 bits (32 bytes), concatenate the hashes and do a final hash of the resultant concatenated 1,048,576 byte data set to get my final 256-bit hash for the entire file.

Is Method 2 any less secure than Method 1, in terms of collisions being more possible and/or probable? Perhaps I should rephrase this question as: Does Method 2 make it easier for an attacker to create a file that hashes to the same hash value as the original file, except of course for the trivial fact that a brute force attack would be cheaper since the hash can be calculated in parallel on N cpus?

Update: I have just discovered that my construction in Method 2 is very similar to the notion of a hash list. However the Wikipedia article referenced by the link in the preceding sentence does not go into detail about a hash list's superiority or inferiority with regard to the chance of collisions as compared to Method 1, a plain old hashing of the file, when only the top hash of the hash list is used.

Michael Goldshteyn
  • 71,784
  • 24
  • 131
  • 181
  • 1
    Your method 2 is known as a hash tree. Skein already includes a mode for tree hashing in its specification (though I suppose not every implementation supports it). – Paŭlo Ebermann Aug 10 '11 at 19:27
  • Also, this is a question which would really good fit on http://cryptography.stackexchange.com/ - could you flag it for migration, please? (Such flags by the original poster are more likely to get fulfilled by the moderators than flags by me.) – Paŭlo Ebermann Aug 10 '11 at 19:29
  • I have posted the question to the cryptography beta site, and will close it here after marking one of the answers as answered over the next two days, to compensate answerers for their effort in researching their answers. – Michael Goldshteyn Aug 10 '11 at 19:57
  • 1
    I think migration (together with the answers) would have been a better way of doing this. But as you want. – Paŭlo Ebermann Aug 10 '11 at 20:00
  • I agree with you in principle and would have migrated, but there were already too many answers from people who deserve credit (on this site) by the time I read your message, to do this at that point. – Michael Goldshteyn Aug 10 '11 at 20:47
  • 2
    Just for reference: The cross-post is now at [Cryptography Stack Exchange](http://crypto.stackexchange.com/q/360/58). – Paŭlo Ebermann Aug 10 '11 at 21:16
  • Questions should be migrated regardless of existing answers if they belong a particular site; [crossposting](http://meta.stackexchange.com/q/64068/156625) is [strongly](http://meta.stackexchange.com/questions/64068/is-cross-posting-a-question-on-multiple-stack-exchange-sites-permitted-if-the-que/64069#64069) [discouraged](http://meta.stackexchange.com/questions/64068/is-cross-posting-a-question-on-multiple-stack-exchange-sites-permitted-if-the-que/64073#64073). – Dave DuPlantis Aug 11 '11 at 21:00
  • Please avoid cross posting in the future. – Tim Post Aug 12 '11 at 08:16

3 Answers3

9

Block-based hashing (your method 2) is a well known technique that is used in practice:

Just like what you're doing, these methods takes the list of block hashes and hashes that again, down to a single short hash. Since this is a well established practice, I would assume that it is as secure as sequential hashing.

Nayuki
  • 17,911
  • 6
  • 53
  • 80
  • There would not be more hashes using method 2, since only the final hash is shared / stored, not the intermediate ones. – Michael Goldshteyn Aug 10 '11 at 18:13
  • The fact that hash trees are named after the famous cryptographer Ralph Merkle may give some authority for its security. – Nayuki Aug 10 '11 at 18:16
  • 1
    The question is not whether Method 2 is secure, it surely is. The question is whether or not Method 2 is strictly less secure than Method 1 and, even if theoretically, by what factor. After all, the gain in performance must be balanced with the loss in security, if any, to be justifiable. – Michael Goldshteyn Aug 10 '11 at 18:57
  • My intuition says that the loss of security is negligible. I acknowledge that because the block size is smaller (1 MB instead of whole file), it might be easier to find a collision or preimage. But at the same time, the block hashes are concealed by the final hash. So I don't know how much the security is affected. – Nayuki Aug 10 '11 at 19:06
  • 1
    From wiki: The Merkle hash root does not indicate the tree depth, enabling a second-preimage attack in which an attacker creates a document other than the original that has the same Merkle hash root. – YoniXw Aug 08 '16 at 21:30
5

Some modern hash designs allow them to be run in parallel. See An Efficient Parallel Algorithm for Skein Hash Functions. If you are willing to use a new (and hence less thoroughly tested) hash algorithm, this may give you the speed increase you want on a multi-processor machine.

Skein has reached the final stage of the NIST SHA-3 competition so it is not completely untested.

rossum
  • 15,344
  • 1
  • 24
  • 38
0

I think it would be significantly easier for an attacker to find a collision, because the time required to generate a hash is a function of the size of the data to hash. One of the great things about cryptographically secure hashes is that an attacker can't take your 100Gb file, find a spot they want to mutate, hash everything before and after that block, and then use those pre-computed values to quickly get the hash of the whole file after small/quick permutations to the bit their interested in. This is because theres an overlapping sliding window in the hashing algorithm.

In short, if you edit the middle of the file, you still need to hash the whole file to get the final checksum. Thus a 100Gb file takes a lot longer to find a collision in, than a 100byte file. The exception is when the edit is nonsense right at the end of the file, which is why that is so frequently seen for 'in-the-wild' in collision examples for large files.

However, if you break your original file up into blocks, the speed of an attack is now a function of the smallest block (or the size of the block you want to mutate). Since file size increases linearly with hashing time, a 100Gb file will take roughly 2000 seconds for each permutation/MD5, while a 1Mb block would allow an attacker to try 50 per second.

The solution would be to break your file up into overlapping chunks, then MD5 those chunks individually. The resultant hash would be a concatenation of the hashes in both start-to-end order, and end-to-start. Now finding a collision requires the whole file to be hashed - albeit in a parallelized way.

J.J
  • 3,459
  • 1
  • 29
  • 35
  • 1
    Note that MD5 is no longer a good hash algorithm and on some platforms SHA-256 is several times faster. "While a 1Mb block would allow an attacker to try 50 per second" what might be the time to a hash collision at that rate. Note: On a lousy iPhone I can perform ~1000 1MB SHA-256 hashes per second. – zaph Mar 24 '16 at 14:37
  • Well, there is a big difference between hashing 1Mb that was created in RAM, and 1Mb read off the disk. But I agree, newer cpu op-code optimizations exist for MD5 and SHA-X. In my hands however, MD5 is always faster than SHA-256. Perhaps im not using the latest software. – J.J Mar 24 '16 at 15:05
  • "While a 1MB block would allow an attacker to try 50 per second" in RAM what might be the time to a hash collision at that rate. Seconds, hours, days, years, eons? I ask this because you propose that a collision is a potential problem so some metric is needed. Note MB is bytes, Mb is bits. – zaph Mar 24 '16 at 15:24
  • Yeah i was being lazy with the notation, but it doesn't really matter either, because my point is the same. Calculating a hash is 10x quicker when the input data is 10x smaller. Since the OP proposes 10s of Gigabytes to 1 Megabyte, this is several orders of magnitude quicker, which is a problem. I don't know what that means practically since it depends on the implementation, the size of the block, the hash you want to collide with, how you want to permute the data, how big is the CPU L2 cache or GPU onboard memory, etc etc.But its definitely going to cause a problem. – J.J Mar 24 '16 at 15:59
  • tldr; collisions are not going to be a problem. Approximate time to finding a collision to a single MD5 hash collision at 50 attempts/sec: (2^127) / (50/sec) = 3.4E36 sec. Converting to a geologic time scale: 100,000,000,000,000,000,000 [eons](https://en.wikipedia.org/wiki/Geologic_time_scale). Faster computers do not really help much. But even this will probably fail if the length of the hash input is constrained. Of course one can always get lucky. (OK, this math is fuzzy but the time is just improbably in any reasonable or unreasonable timeframe. Any have the correct math?) – zaph Mar 24 '16 at 16:47