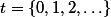Converting 2-3-4 to Red-Black Tree

Question

I am familiar with converting individual 2-node, 3-node, and 4-nodes straight to Red-Black trees. And this Stackoverflow link is a good explanation 2-3-4 to Red-Black. However, I have a question about the example given in that link. This is how the Stackoverflow question 2-3-4 to red-black was illustrated 2-3-4 to Red-Black

I highlighted the part that I am questioning. Why is it on this guide 4-node connected to 2-node I found and others on the internet, they say when encountering a 4 node connected to a 2 or 3 node, you need to switch the colors around. But in the StackOverflow example that I highlighted red, they didn't. Thanks

Answer 1

The following image does not imply that the colors of the red-back tree need to be swapped:

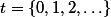
It merely describes the process of splitting a B-tree node, which leads to an alternative B-tree for the same data.

Then it shows how that different shape of the B-tree leads to a different coloring in the corresponding red-black tree, and how that new coloring is also a valid alternative.

But the translation from B-tree to red-black tree follows the rules you referred to:

If we look at the left side of the image, we see at the bottom layer of the B-tree a 4-node. According to the rules, this translates to a black node (c) with two red children (b and d). The 2-node at the root translates to a black node (a).

If we look at the right side of the image, we see two 2-nodes at the bottom layer of the B-tree. These translate each to a back node (b and d). The root 3-node is translated to a back node (a) with a red node (c) as child.

This is exactly what is depicted at the bottom of the image. The point is that these two variants are valid red-black trees for the same data, but derived from different shapes of B-trees.

Such a transition from the left to the right version might be needed when inserting a node. For instance, if an "e" would be added, then it cannot be added as a child of the "d" node in the red-black tree without recoloring. By switching to the right-side version of the red-black tree, the node can be added as (red) child of node "d".