A standard offsetting algorithm would work as follows:
- Consider the line segments to be full lines. Offset all of them in the chosen direction by the given amount.
- Find the intersection of each pair of neighboring lines. That will be the new positions of the vertices.
- Check for vanishing segments and remove the respective vertices.
Note that Jerome's code offsets points, not segments. So you observed correctly that it fails to keep a fixed distance for very sharp angles. It also ignores the third step completely.
Now the difficult part is how to include a variable offset into this? If you had offset weights for each segment, it would be straight forward to integrate. But in your question you state that you have offset weights per vertex. Simply adding a 4th step that would move around the obtained vertices would invalidate the results of step 3. So I would rather search for a way to integrate the variable offset to the first step. In fact correct representation would require not only to offset the lines, but also rotating them. They would of course be no more parallel, but in my opinion this would represent the variable vertex offset nature the best. Again, if you want to reduce such difficulties, think about using per-segment weights which makes the whole problem much easier, since a weighted line offset can be easily integrated into step 1.
Update
I fixed and extended the example from Jerome's answer. @Jerome, thank you for introducing me to paper.js and for the initial inspiration. In my version I use variable widths per-segment, as a ratio of the fixed offset. Try it out here.
//the paper.js is really stupid: the search is hidden by the execution controls
//and once I rename this class to "Line" which would be more appropriate
//(but my original intent was indeed a Halfline), it throws errors, //so I keep the slightly misleading name "Halfline"
class Halfline {
constructor(p, r)
{
const tangent = r - p;
this.p = p;
this.r = r;
//implicit line equation
this.a = -tangent.y;
this.b = tangent.x;
this.c = p.x * this.a + p.y * this.b;
//I didn't normalize a and b, so here a unit normal
this.n = new Point(this.a, this.b);
this.n /= this.n.length;
}
//offset the line by t in the direction of its normal
offset(t) {
return new Halfline(this.p + this.n * t, this.r + this.n * t)
}
//line intersection (infinite lines)
intersect(other) {
const det = this.a * other.b - other.a * this.b;
if (Math.abs(det) < 1e-5) //parallel
return undefined;
const x = (other.b * this.c - this.b * other.c) / det;
const y = (this.a * other.c - other.a * this.c) / det;
return new Point(x, y);
}
}
//look at this great tutorial for details on helper functions:
//https://algorithmtutor.com/Computational-Geometry/Check-if-two-Halfline-segment-intersect/
function fixOverlaps(polyline) {
function on_segment(p1, p2, p) {
return Math.min(p1.x, p2.x) <= p.x
&& p.x <= Math.max(p1.x, p2.x)
&& Math.min(p1.y, p2.y) <= p.y
&& p.y <= Math.max(p1.y, p2.y);
}
function cross_product(p1, p2) {
return p1.x * p2.y - p2.x * p1.y;
}
function direction(p1, p2, p3) {
return cross_product(p3 - p1, p2 - p1);
}
function segmentsIntersect(p1, p2, p3, p4) {
d1 = direction(p3, p4, p1);
d2 = direction(p3, p4, p2);
d3 = direction(p1, p2, p3);
d4 = direction(p1, p2, p4);
return ( (((d1 > 0 && d2 < 0) || (d1 < 0 && d2 > 0))
&& ((d3 > 0 && d4 < 0) || (d3 < 0 && d4 > 0)))
|| (d1 == 0 && on_segment(p3, p4, p1))
|| (d2 == 0 && on_segment(p3, p4, p2))
|| (d3 == 0 && on_segment(p1, p2, p3))
|| (d4 == 0 && on_segment(p1, p2, p4)) );
}
//search for self-intersections
let intersectionsFound = true;
while (intersectionsFound)
{
let result = [polyline[0]];
for(let i = 1; i < polyline.length; ++i)
{
let anyIntersection = false;
for(let j = i + 2; j < polyline.length; ++j)
if (segmentsIntersect(polyline[i-1], polyline[i], polyline[j-1], polyline[j]))
{
const s = new Halfline(polyline[i-1], polyline[i]);
const t = new Halfline(polyline[j-1], polyline[j]);
result.push(s.intersect(t))
anyIntersection = true;
i = j;
break;
}
result.push(polyline[i])
}
intersectionsFound = polyline.length > result.length;
polyline = result;
}
return polyline;
}
const points = [
new Point(30, 40),
new Point(100, 200),
new Point(200, 60),
new Point(250, 50),
new Point(300, 70),
new Point(350, 250),
new Point(400, 60),
new Point(450, 50),
new Point(500, 70),
new Point(550, 90),
];
let poly1 = new Path();
poly1.strokeColor = 'black';
points.forEach(p => poly1.add(p));
const fixOffs = 10;
const offsets = [1, 2, 3, 2, 1, 0.5, 2.5, 2, 3, 1].map(x => x * fixOffs);
let fix = [];
let variable = [];
const size = points.length;
for(let i = 0; i < size; ++i){
let normal;
if(i == 0 || i == size - 1) { // first or last
const tangent = i == 0 ? points[i + 1] - points[i] : points[i] - points[i - 1];
const normal = new Point(-tangent.y, tangent.x) / tangent.length;
fix.push(points[i] + normal * fixOffs);
variable.push(points[i] + normal * offsets[i]);
} else {
const prevSegment = new Halfline(points[i - 1], points[i]);
const nextSegment = new Halfline(points[i], points[i + 1]);
//CONSTANT
const newConstVertex = prevSegment.offset(fixOffs).intersect(nextSegment.offset(fixOffs));
fix.push(newConstVertex || (points[i] + prevSegment.n * fixOffs));
//VARIABLE
const newVarVertex = prevSegment.offset(offsets[i]).intersect(nextSegment.offset(offsets[i + 1]));
variable.push(newVarVertex || (points[i] + prevSegment.n * offsets[i]));
}
}
//Resolve vanishing segments
const finalFix = fixOverlaps(fix);
const finalVar = fixOverlaps(variable);
let polyFix = new Path();
polyFix.strokeColor = 'red';
finalFix.forEach(p => polyFix.add(p));/**/
let polyVar = new Path();
polyVar.strokeColor = 'green';
finalVar.forEach(p => polyVar.add(p));/**/
Note that it still does not handle all special cases. For example the corners of a non-closed polyline will produce strange shapes once the offset grows too large. Also note that the last two segments are parallel, an interesting choice of Jerome and good for debugging. I assigned them a different offset which forces the segments to give up their parallelity.
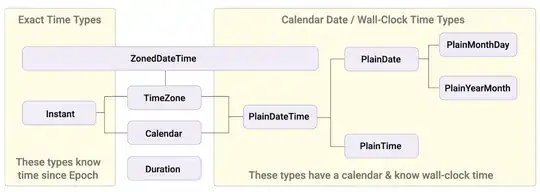 The above image almost encapsulates what I want to do; the only thing is, it is uniform offset throughout the polylines, whereby I want variable offset.
The above image almost encapsulates what I want to do; the only thing is, it is uniform offset throughout the polylines, whereby I want variable offset.