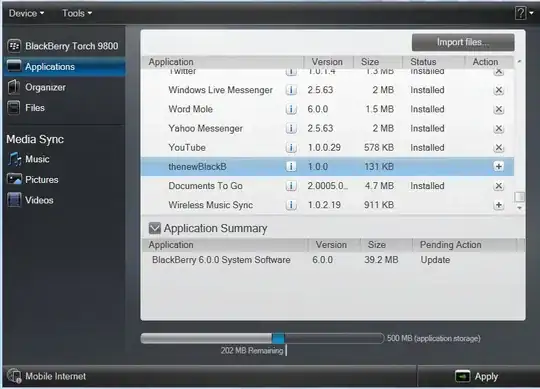
The script below is a mixture of stackoverflow answers on different topics, but closely related to finding peaks on signals. Finding peaks based on prominence, as noted here works incredibly well, but my issue is that I need to find the lowest point immediately after the peak. The dataset is a fluorescence signal of a plant captured during 14 continuous hours, and the peaks are saturating pulses used to determined saturation under light conditions. A picture of the dataset (a 68MB CSV file) bellow:
This is my python script:
import pandas as pd
import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt
from scipy.signal import find_peaks
# A parser is required to translate the timestamp
custom_date_parser = lambda x: datetime.strptime(x, "%d-%m-%Y %H:%M_%S.%f")
df = pd.read_csv('15-01-2022_05_00.csv', parse_dates=[ 'Timestamp'], date_parser=custom_date_parser)
x = df['Timestamp']
y = df['Mean_values']
# As per accepted answer here:
#https://stackoverflow.com/questions/1713335/peak-finding-algorithm-for-python-scipy
peaks, _ = find_peaks(y, prominence=1)
# Invert the data to find the lowest points of peaks as per answer here:
#https://stackoverflow.com/questions/61365881/is-there-an-opposite-version-of-scipy-find-peaks
valleys, _ = find_peaks(-y, prominence=1)
print(y[peaks])
print(y[valleys])
plt.subplot(2, 1, 1)
plt.plot(peaks, y[peaks], "ob"); plt.plot(y); plt.legend(['Prominence'])
plt.subplot(2, 1, 2)
plt.plot(valleys, y[valleys], "vg"); plt.plot(y); plt.legend(['Prominence Inverted'])
plt.show()
As you can see on the picture, not all the 'prominence inverted' points are below the respective peak. The prominence inverted function comes from this post here, and it simply inverts the dataset. Some are adjacent to the previous peak (difficult to see in the picture). Peaks and valleys below:
Peaks
1817 109.587178
3674 89.191393
56783 72.779385
111593 77.868118
166403 83.288949
221213 84.955026
276023 84.340550
330833 83.186605
385643 81.134827
440453 79.060960
495264 77.457803
550074 76.292243
604884 75.867575
659694 75.511924
714504 74.221657
769314 73.830941
824125 76.977637
878935 78.826169
933745 77.819844
988555 77.298089
1043365 77.188105
1098175 75.340765
1152985 74.311185
1207796 73.163844
1262606 72.613317
1317416 73.460068
1372226 70.388324
1427036 70.835355
1481845 70.154085
Valleys
2521 4.669368
56629 26.551585
56998 26.184984
111791 26.288734
166620 27.717165
221434 28.312708
330432 28.235397
385617 27.535091
440341 26.886589
495174 26.379043
549353 26.040947
550239 25.760023
605051 25.594147
714352 25.354300
714653 25.008184
769472 24.883584
824284 25.135316
879075 25.477464
933907 25.265173
988711 25.160046
1097917 25.058851
1098333 24.626667
1153134 24.357835
1207943 23.982878
1262750 23.938298
1371013 23.766077
1372381 23.351263
1427187 23.368314
Any ideas about this awkward result on the valleys?