I wrote a program in Python to solve the 1D wave equation by treating it as a first-order in time linear system, where the spatial variables are discretized (using 2nd order methods) and I integrate in time using a 4th-order Runge-Kutta.
My problem is: when I compute the order of convergence at each time-step, it is roughly equal to 2 for small times, and then gets worse for larger times. Here is a plot (on the y-axis is the L^2 norm of the order of convergence):
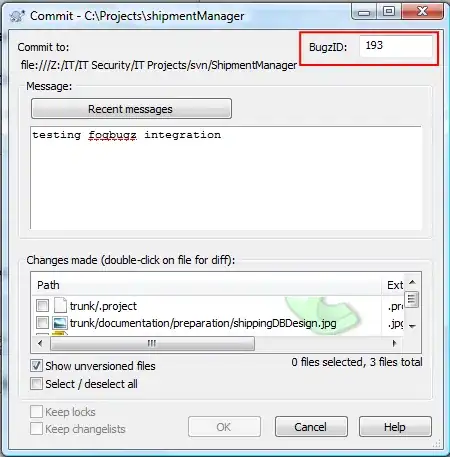
In the above I used a spatial grid in the interval [0, 1] with grid interval 0.5, and 10000 time iterations for Runge-Kutta. I computed the solution at the final time T = 0.8 s and thus the time interval was T/10000. I considered periodic boundary conditions for the solutions.
My code to compute the order of convergence is the following:
def orderOfConvergence(u, u2, u3, length, f):
num = 0
den = 0
for i in range(0, length):
den += (u[i] - u2[int(i/f)])**2
num += (u2[int(i/f)] - u3[int(i/(f**2))])**2
if den > 0 and num > 0:
return 0.5*log(num/den, f)
else:
return 0
where u, u2 and u3 are the three solutions computed with finer and finer grids. In my code, f=0.5, since halved the grid interval each time.
What might be the cause for such a behaviour?