How to get a smoothed contour line in matplotlib given non-smooth underlying data

Question

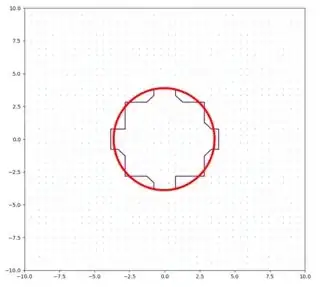
I have boolean data on a 2D grid and want to use matplotlib to plot a countour between the areas where the data is True and False.

However, the separation between these areas is not smooth within the actual data. How can I compute a smoothed countour given this data?

Here is a minimal example:

import numpy as np
import matplotlib.pyplot as plt

# generate some non-smooth example data
MESHSIZE = 10
REFINEMENT = 4*MESHSIZE
x = np.linspace(-MESHSIZE, MESHSIZE, REFINEMENT)
xv, yv = np.meshgrid(x, x)
xvf = xv.reshape(-1)
yvf = yv.reshape(-1)


def choppy_circle(x, y):
    inner = x.astype(int)**2+y.astype(int)**2 < 10.0
    return inner


# consider this the *actual* data given to me as-is
my_x = xvf
my_y = yvf
my_z = choppy_circle(xvf, yvf)

# need to visualize the contour that separates areas where
# my_z is True/False
plt.tricontour(my_x, my_y, my_z, levels=np.array([1.0-1e-3]))
plt.scatter(xv, yv, s=0.1)
plt.show()

This produces the following plot, which is faithful to the data, but not what I'm looking for:

How can I use the data given in my_x, my_y and my_z to construct a smoothed contour around the domain where my_z is True?

Something like this:

A (hand drawn if need be) example of what you expect would be helpful ;) — mozway, Jan 16 '22 at 16:02
you can get the coordinates of the points making the line and use `shapely` to determine the center of gravity and bounding box/circle — mozway, Jan 16 '22 at 17:30
Good hint, I got the contour vertices using `cs.collections[0].get_paths()` where `cs = plt.tricontour(my_x, my_y, my_z, levels=np.array([1.0-1e-3]))`. Interpolating them like @user2640045 suggested might do the trick. I'll check and come back. — Christoph90, Jan 17 '22 at 09:40

score 2 · Answer 1 · answered Jan 16 '22 at 20:03

2

You can fit a spline to the contour. And make it as smooth as you want by picking the spline's smoothing parameter.

First you obtain the boundary points

import functools
import itertools

mask = my_z.reshape(40,40)
mask &= functools.reduce(np.logical_or,[~np.roll(np.roll(mask, shift_x, 0),shift_y,1) 
                                            for shift_x,shift_y in itertools.product((-1,0,1),repeat=2)])
x,y = my_x[mask.reshape(-1)],my_y[mask.reshape(-1)]
plt.scatter(x,y)

Now we sort your points by the argument of the corresponding complex number. If you don't know what I mean by that it's the angle the point makes with the origin and the point (1,0). And fit a spline to it.

import scipy.interpolate as interpolate
import matplotlib.pyplot as plt

arr = np.array(sorted(zip(x,y), key=lambda x: cmath.phase(x[0]+1j*x[1])))
s=1

tck, u = interpolate.splprep([arr[:,0],arr[:,1]],per=1, s=s)
x_i, y_i = interpolate.splev(np.linspace(0, 1, 10**4), tck)
ax = plt.gca()
ax.plot(x_i, y_i)
ax.scatter(arr[:,0],arr[:,1])
ax.set_title(f"{s=}")
ax.set_aspect('equal')

The results look differently depending on s. I plotted it for a few for you:

answered Jan 16 '22 at 20:03

Lukas S

3,212
2
13
25

This is a great and crafty approach! However, due to the reliance on the complex argument, it seems that it only will work for data that defines a single star-convex set that contains the coordinate origin (which i encouraged by the simple example data!). I was hoping for something that would work for contouring arbitrary multiply connected sets if thats possible at all in an automized way. – Christoph90 Jan 17 '22 at 09:10
@Christoph90 being "crafty" is way easier when you provide an example. So if you want me to change my code to your new needs it would be nice if you provided an example. – Lukas S Jan 18 '22 at 10:43
You are right, however, its not obvious how to construct non-trivial example data without just uploading my actual data. Since I could find a solution using the x-y data from `tricontour` and the interpolation strategy you recommended, I've posted that below instead of further pondering on the example data. – Christoph90 Jan 18 '22 at 16:48
Big thanks and +1 though for your answer, it contained everything relevant, just needed to get the contour data from `tricontour` instead. – Christoph90 Jan 18 '22 at 16:52

score 1 · Answer 2 · answered Jan 17 '22 at 15:09

1

You can use shapely to get the centroid and bounding box of your arbitrary shape, then plot a circle:

# […] same as previously

# get points
cs = plt.tricontour(my_x, my_y, my_z, levels=np.array([1.0-1e-3]))
v = cs.collections[0].get_paths()[0].vertices

from shapely.geometry import Polygon

# find centroid coordinates and bounding box
p = Polygon(v)
x,y =p.centroid.coords[0]
minx, miny, maxx, maxy = p.bounds

# plot circle
# depending on the data, one could also plot an ellipse or rectangle
r = max((maxx-minx)/2, (maxy-miny)/2)
circle = plt.Circle((x, y), r, color='r', fill=False)
plt.gca().add_patch(circle)

output:

answered Jan 17 '22 at 15:09

mozway

194,879
13
39
75

Thanks, this is very interesting and `shapely` seems *very* feature-rich. I should have provided other example data, as the circular distribution set a wrong track. – Christoph90 Jan 18 '22 at 16:54
@Christoph90 I don't fully understand the ultimate goal. Maybe provide other examples. That said, as I commented in my answer, you can also use other kinds of bounding shapes (a rectangle would always contain all points). – mozway Jan 18 '22 at 16:56
The ultimate goal is not to rely on the bounding shape being circular, rectangular or some other special geometry but to smooth contour lines of arbitrary geometry. – Christoph90 Jan 19 '22 at 08:16

score 0 · Accepted Answer · answered Jan 18 '22 at 16:45

Extracting the contour data like proposed in this answer and interpolating with splines as proposed by @user2640045 allows doing it for arbitrary contours:

# my_x, my_y, my_z as above...

# get contour data
cs = plt.tricontour(my_x, my_y, my_z, levels=np.array([1.0-1e-3]))
print(type(cs))

# process each contour
for contour in cs.collections[0].get_paths():
    vert = contour.vertices
    vert_x = vert[:, 0]
    vert_y = vert[:, 1]

    # plot contour
    plt.plot(vert_x, vert_y)

    # interpolate contour points
    s = 20
    tck, u = interpolate.splprep([vert_x, vert_y], per=1, s=s)
    x_interp, y_interp = interpolate.splev(np.linspace(0, 1, 10**3), tck)

    # plot interpolated contour
    plt.plot(x_interp, y_interp)

# plot grid
plt.scatter(xv, yv, s=0.1)

# display plot
plt.show()

The important bit is the loop header

for contour in cs.collections[0].get_paths():

where the x-y data of each contour line is obtained.

How to get a smoothed contour line in matplotlib given non-smooth underlying data

3 Answers3