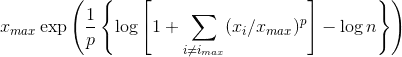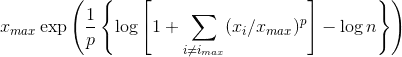
The DFT (FFT being its algorithmic computation) is a dot product between a finite discrete number of samples N of an analogue signal s(t) (a function of time or space) and a set of basis vectors of complex exponentials (sin and cos functions). Although the sample is naturally finite and may show no periodicity, it is implicitly thought of as a periodically repeating discrete function. Even when dealing with real-valued signals (the usual situation) it is convenient to work with complex numbers (Euler's equation). It may be intimidating to implement the function on a signal with np.fft.fft(s) only to get the output coefficients in complex numbers and get stuck in their interpretation. Some steps are essential:
What are the frequencies in the complex exponentials?
- The DFT does not necessarily preserve the sampling frequency in Hertz. The frequencies are indices (k).
- The indices k range from
0 to N - 1 and can be thought of as having units of cycles / set (the set being the N samples of the signal s). I will omit discussing the Nyquist limit, but for real signals the frequencies form a mirror image after N / 2, and given as negative decreasing values after that point (not a problem within the framework of implicit periodicity). The frequencies used in the FFT are not simply k, but k / N, thought of as having units of cycles / sample. See this reference. Example (reference): If a signal is sampled N = 5 times the frequencies are: np.fft.fftfreq(5), yielding [ 0 , 0.2, 0.4, -0.4, -0.2], i.e. [0/5, 1/5, 2/5, -2/5, -1/5].
- To convert these frequencies to meaningful units (e.g. Hetz or mm) the values in cycles/sample above will need to be divided by sampling interval T (e.g. distance in seconds between samples). Continuing with the example above, there is a built-in call:
np.fft.fftfreq(5, d=T): If the analogue signal s is sampled 5 times at equidistant intervals T = 1/2 sec for a total sample of NT = 5 x 1/2 sec, the normalized frequencies will be np.fft.fftfreq(5, d = 1/2), yielding [0 0.4 0.8 -0.8 -0.4] or [0/NT, 1/NT, 2/NT, -2/NT, -1/NT].
- Either normalized or un-normalized frequencies are used to control angular frequencies (ω_m), expressed as ω_m = 2π k/NT. Note that
NT is the total duration for
which the signal was sampled. The index k does result in multiples of a fundamental frequency (ω-naught) corresponding to k = 1 - the frequency of (co-)sine wave that completes
exactly one oscillation over NT (here).
Magnitude, frequency and phase of the coefficients in the FFT
- Given the output of the FFT
S = fft.fft(s), the magnitude of the output coefficients (here) is just the Euclidean norm of the complex numbers in the output coefficients adjusted for the symmetry in real signals (x 2) and for the number of samples 1/N: magnitudes = 1/N * np.abs(S)
- The frequencies are matched to the call explained above
np.fft.fftfreq(N), or more expediently to incorporate the actual analogue frequency units, frequencies = np.fft.fftfreq(N, d=T).
- The phase of each coefficients is the angle of the complex number in polar form
phase = np.arctan(np.imag(S)/np.real(S))
How to find the dominant frequencies in the signal s in the FFT and their coefficients?
- Plotting aside, finding the index
k corresponding the frequency with the highest magnitude can be accomplished as index = np.argmax(np.abs(S)). To find the 4 indices with the highest magnitude, for example, the call is indices = np.argpartition(S,-4)[-4:].
- And finding the actual corresponding coefficient:
S[index] with frequency freq_max = np.fft.fftfreq(N, d=T)[index].
Reproducing the original signal after obtaining the coefficients:
Reproducing s through sines and cosines (p.150 in here):
Re = np.real(S[index])
Im = np.imag(S[index])
s_recon = Re * 2/N * np.cos(-2 * np.pi * freq_max * t) + abs(Im) * 2/N * np.sin(-2 * np.pi * freq_max * t)
Here is a complete example:
import numpy as np
import matplotlib.pyplot as plt
N = 10000 # Sample points
T = 1/5000 # Spacing
# Total duration N * T= 2
t = np.linspace(0.0, N*T, N, endpoint=False) # Time: Vector of 10,000 elements from 0 to N*T=2.
frequency = np.fft.fftfreq(t.size, d=T) # Normalized Fourier frequencies in spectrum.
f0 = 25 # Frequency of the sampled wave
phi = np.pi/8 # Phase
A = 50 # Amplitude
s = A * np.cos(2 * np.pi * f0 * t + phi) # Signal
S = np.fft.fft(s) # Unnormalized FFT
index = np.argmax(np.abs(S))
print(S[index])
magnitude = np.abs(S[index]) * 2/N
freq_max = frequency[index]
phase = np.arctan(np.imag(S[index])/np.real(S[index]))
print(f"magnitude: {magnitude}, freq_max: {freq_max}, phase: {phase}")
print(phi)
fig, [ax1,ax2] = plt.subplots(nrows=2, ncols=1, figsize=(10, 5))
ax1.plot(t,s, linewidth=0.5, linestyle='-', color='r', marker='o', markersize=1,markerfacecolor=(1, 0, 0, 0.1))
ax1.set_xlim([0, .31])
ax1.set_ylim([-51,51])
ax2.plot(frequency[0:N//2], 2/N * np.abs(S[0:N//2]), '.', color='xkcd:lightish blue', label='amplitude spectrum')
plt.xlim([0, 100])
plt.show()
Re = np.real(S[index])
Im = np.imag(S[index])
s_recon = Re*2/N * np.cos(-2 * np.pi * freq_max * t) + abs(Im)*2/N * np.sin(-2 * np.pi * freq_max * t)
fig = plt.figure(figsize=(10, 2.5))
plt.xlim(0,0.3)
plt.ylim(-51,51)
plt.plot(t,s_recon, linewidth=0.5, linestyle='-', color='r', marker='o', markersize=1,markerfacecolor=(1, 0, 0, 0.1))
plt.show()
s.all() == s_recon.all()