This is a question about taking multiple rankings of the same elements and computing a statistic that depends on whether each possible inversion matches between one or more lists or not.
Given
- L equal-length lists of length N comprising the first N integers in various orders
- an arbitrary set of L weights
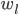, one corresponding to each list - some arbitrary non-linear scalar function f
I'd like to compute in O(L N log N) time (it's trivial to do in O(L N^2) time) the following quantity:
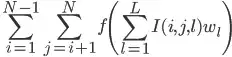
where
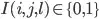represents whether the integer i appears before the integer j in list l .
Is there a known algorithm for doing this? Or is it known to be impossible in O(L N log N) time?
So far I've found a binary-indexed trees inversion counting algorithm and I'm wondering if I could get what I need by building upon this idea.
