Solve loop data dependency with SIMD - finding transitions between -1 and +1 in an int8_t array of sgn values

Question

I try to achieve performance improvement and made some good experience with SIMD. So far I was using OMP and like to improve my skills further using intrinsics.

In the following scenario, I failed to improve (even vectorize) due to a data dependency of a last_value required for a test of element n+1.

Environment is x64 having AVX2, so want to find a way to vectorize and SIMDfy a function like this.

inline static size_t get_indices_branched(size_t* _vResultIndices, size_t _size, const int8_t* _data) {
    size_t index = 0;
    int8_t last_value = 0;
    for (size_t i = 0; i < _size; ++i) {
        if ((_data[i] != 0) && (_data[i] != last_value)) {
            // add to _vResultIndices
            _vResultIndices[index] = i;
            last_value = _data[i];
            ++index;
        }
    }
    return index;
}

Input is an array of signed 1-byte values. Each element is one of <0,1,-1>. Output is an array of indices to input values (or pointers), signalling a change to 1 or -1.

example in/output

in: { 0,0,1,0,1,1,-1,1, 0,-1,-1,1,0,0,1,1, 1,0,-1,0,0,0,0,0, 0,1,1,1,-1,-1,0,0, ... }
out { 2,6,7,9,11,18,25,28, ... }

My first attempt was, to play with various branchless versions and see, if auto vectorization or OMP were able to translate it into a SIMDish code, by comparing assembly outputs.

example attempt

int8_t* rgLast = (int8_t*)alloca((_size + 1) * sizeof(int8_t));
rgLast[0] = 0;

#pragma omp simd safelen(1)
for (size_t i = 0; i < _size; ++i) {
    bool b = (_data[i] != 0) & (_data[i] != rgLast[i]);
    _vResultIndices[index] = i;
    rgLast[i + 1] = (b * _data[i]) + (!b * rgLast[i]);
    index += b;
}

Since no experiment resulted in SIMD output, I started to experiment with intrinsics with the goal to translate the conditional part into a mask.

For the != 0 part that's pretty straight forward:

__m256i* vData = (__m256i*)(_data);
__m256i vHasSignal = _mm256_cmpeq_epi8(vData[i], _mm256_set1_epi8(0)); // elmiminate 0's

The conditional aspect to test against "last flip" I found not yet a way.

To solve the following output packing aspect I assume AVX2 what is the most efficient way to pack left based on a mask? could work.

Update 1

Digging deeper into this topic reveals, it's beneficial to separate the 1/-1's and get rid of the 0's. Luckily in my case, I can directly grab this from pre-processing and skip processing to <1,0,-1> using _mm256_xor_si256's for example, having 2 input vectors separated as gt0 (all 1's) and lt0 (all -1's). This also allows 4 times tighter packing of data.

I might want to end up with a process like this 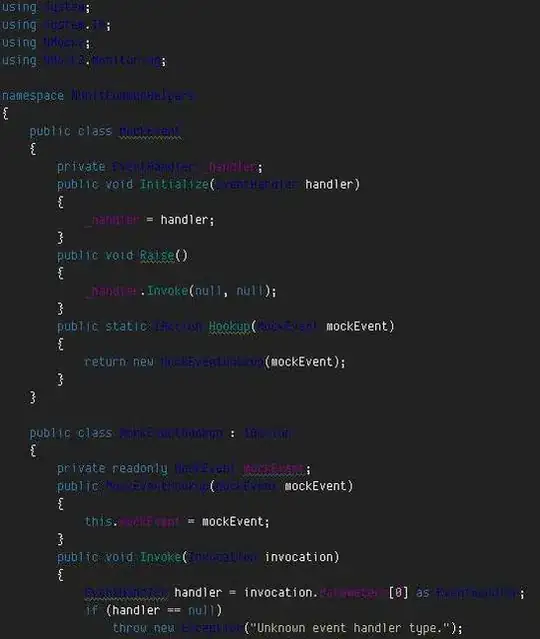The challenge now is how to create the transition mask based on gt0 and lt0 masks.

Update 2

Appearently an approach of splitting 1's and -1's into 2 streams (see in answer how), introduces a dependency while acessing elements for scanning alternating: How to efficiently scan 2 bit masks alternating each iteration

Creation of a transition mask as @aqrit worked out using
transition mask = ((~lt + gt) & lt) | ((~gt + lt) & gt) is possible. Eventhough this adds quite some instructions, it apears to be a beneficial tradeoff for data dependency elimination. I assume the gain grows the larger a register is (might be chip dependent).

Update 3

By vectorizing transition mask = ((~lt + gt) & lt) | ((~gt + lt) & gt) I could get this output compiled

vmovdqu     ymm5,ymmword ptr transition_mask[rax]  
vmovdqu     ymm4,ymm5  
vpandn      ymm0,ymm5,ymm6  
vpaddb      ymm1,ymm0,ymm5  
vpand       ymm3,ymm1,ymm5  
vpandn      ymm2,ymm5,ymm6  
vpaddb      ymm0,ymm2,ymm5  
vpand       ymm1,ymm0,ymm5  
vpor        ymm3,ymm1,ymm3  
vmovdqu     ymmword ptr transition_mask[rax],ymm3

On first look it appears efficient compared to potential condition related pitfalls of post-processing (vertical scan + append to output), although it appears to be right and logical to deal with 2 streams instead of 1.

This lacks the ability to generate the initial state per cycle (transition from 0 to either 1 or -1). Not sure if there is a way to enhance the transition_mask generation "bit twiddling", or use auto initial _tzcnt_u32(mask0) > _tzcnt_u32(mask1) as Soons uses here: https://stackoverflow.com/a/70890642/18030502 which appears to include a branch.

Conclusion

The approach @aqrit shared using an improved bit-twiddling solution per chunk load to find transitions, turns out to be the most runtime performant. The hot inner loop is just 9 asm instructions long (per 2 found items for comparison with other approaches) using tzcnt and blsr like this

tzcnt       rax,rcx  
mov         qword ptr [rbx+rdx*8],rax  
blsr        rcx,rcx  
tzcnt       rax,rcx  
mov         qword ptr [rbx+rdx*8+8],rax  
blsr        rcx,rcx  
add         rdx,2  
cmp         rdx,r8  
jl          main+2580h (...)  

Answer 1

Complete vectorization is suboptimal for your case. It’s technically possible, but I think the overhead of producing that array of uint64_t values (I assume you’re compiling for 64 bit CPUs) will eat all the profit.

Instead, you should load chunks of 32 bytes, and immediately convert them to bit masks. Here’s how:

inline void loadBits( const int8_t* rsi, uint32_t& lt, uint32_t& gt )
{
    const __m256i vec = _mm256_loadu_si256( ( const __m256i* )rsi );
    lt = (uint32_t)_mm256_movemask_epi8( vec );
    const __m256i cmp = _mm256_cmpgt_epi8( vec, _mm256_setzero_si256() );
    gt = (uint32_t)_mm256_movemask_epi8( cmp );
}

The rest of your code should deal with these bitmaps. To find first non-zero element (you only need to do that at the start of your data), scan for least significant set bit in (lt | gt) integer. To find -1 number, scan for least significant set bit in lt integer, to find +1 number scan for least significant set bit in gt integer. Once found and handled, you can either clear low portion of both integers with bitwise AND, or shift them both to the right.

CPUs have BSF instruction which scans for the lowest set bit in an integer, and returns two things at once: a flag telling if the integer was zero, and the index of that set bit. If you’re using VC++ there’s _BitScanForward intrinsic, otherwise use inline ASM, that instruction is only exposed in VC++; GCC’s __builtin_ctz is not quite the same thing, it only returns a single value instead of two.

However, on AMD CPUs, the TZCNT instruction from BMI 1 set is somewhat faster than the old-school BSF (on Intel they’re equal). On AMD, TZCNT will probably be slightly faster, despite the extra instruction to compare with 0.

Answer 2

Carrying state serially between 64-bit SIMD lanes is more expensive than carrying state serially between 64-bit general purpose registers (gpr).

In practice, lookup-tables (or SIMD left-packing) is limited to processing 8 elements at a time. If the data averages about 6 kept elements per 64 elements then left-packing wastes a lot of processing (especially if we're collecting offsets and not doing a gather operation). If the bitset is dense then consider moving to lookup-tables.

As @Snoots suggests, use SIMD to create 64-bit bitsets and use bitscan intrinsics find the indices of wanted set bits.

Branch misprediction:

Squash the greater-than (gt) and less-than (lt) bitsets into a single bitset using transition_mask = ((~lt + gt) & lt) | ((~gt + lt) & gt) or this simplification from @FalkHüffner transition_mask = (lt ^ (lt - gt)) & (gt ^ (gt – lt)).

The state is carry-in/carry-out for one of the arithmetic ops. I’d be careful using _subborrow_u64 as it is fairly uncommon intrinsic (and is buggy on old compilers).

Which leaves the only remaining branch looping over the bitscan operation. All set bits have to be extracted.. but we can unroll the operation and overshoot to make the branch more predictable. The amount of overshoot needs to be tuned to the expected data set.

Not tested. Asm not inspected.

#include <immintrin.h>
#include <stdint.h>

static inline
uint64_t get_mask (int8_t* src, unsigned char* state) {
    __m256i src0 = _mm256_loadu_si256((__m256i*)(void*)src);
    __m256i src1 = _mm256_loadu_si256((__m256i*)(void*)&src[32]);

    uint64_t lt = (uint32_t)_mm256_movemask_epi8(src0) |
                    (((uint64_t)(uint32_t)_mm256_movemask_epi8(src1)) << 32);

    src0 = _mm256_cmpgt_epi8(src0, _mm256_setzero_si256());
    src1 = _mm256_cmpgt_epi8(src1, _mm256_setzero_si256());

    uint64_t gt = (uint32_t)_mm256_movemask_epi8(src0) |
                    (((uint64_t)(uint32_t)_mm256_movemask_epi8(src1)) << 32);

    // if borrow then greater-than span extends past the msb
    uint64_t m;
    unsigned char s = *state;
    *state = _subborrow_u64(s, lt, gt, (unsigned long long*)&m); // sbb
    return (m ^ lt) & ((gt - (lt + !s)) ^ gt);
}

static inline
size_t bitset_to_index (uint64_t* dst, uint64_t base, uint64_t mask) {
    int64_t cnt = _mm_popcnt_u64(mask);
    int64_t i = 0;
    do { // unroll to taste...
        dst[i + 0] = base + _tzcnt_u64(mask); mask = _blsr_u64(mask);
        dst[i + 1] = base + _tzcnt_u64(mask); mask = _blsr_u64(mask);
        dst[i + 2] = base + _tzcnt_u64(mask); mask = _blsr_u64(mask);
        dst[i + 3] = base + _tzcnt_u64(mask); mask = _blsr_u64(mask);
        i += 4;
    } while (i < cnt);
    return (size_t)cnt;
}

static
uint64_t* get_transition_indices (uint64_t* dst, int8_t* src, size_t len) {
    unsigned char state = 0; // in less-than span
    uint64_t base = 0; // offset into src array
    size_t end = len / 64;
    for (size_t i = 0; i < end; i++) {
        uint64_t mask = get_mask(src, &state);
        src += 64;
        dst += bitset_to_index(dst, base, mask);
        base += 64;
    }
    if (len % 64) {
        ; // todo: tail loop
    }
    return dst;
}