Plot two gaussian distributions out of the data using gaussian mixture model (not a repeated question)

Question

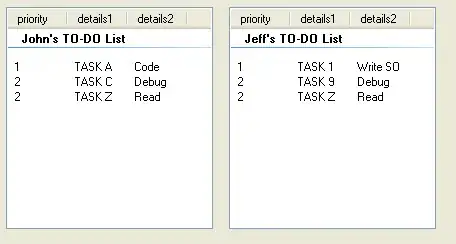
I am having the same problem as this post. I followed @B.M.'s code. However, I am not able to figure out how to fit two gaussian distributions in my data. When I hist-plot it and superimpose it with the KDE, I obtain the second peak like this:

Second peak detected by the slight bump at ~0.07 units

Here are my efforts so far:

from pylab import *
from scipy.optimize import curve_fit

#data=concatenate((normal(1,.2,5000),normal(2,.2,2500)))
data = pd.read_csv('gmm_outdata_ngc2173.csv')
gmm_3 = data['col3']
y,x,_=hist(gmm_3,22,alpha=.3,label='data')

x=(x[1:]+x[:-1])/2 # for len(x)==len(y)

def gauss(x,mu,sigma,A):
    return A*exp(-(x-mu)**2/2/sigma**2)

def bimodal(x,mu1,sigma1,A1,mu2,sigma2,A2):
    return gauss(x,mu1,sigma1,A1)+gauss(x,mu2,sigma2,A2)

expected=(-0.15,.02,22,0.15,.02,22)
params,cov=curve_fit(bimodal,x,y,expected)
sigma=sqrt(diag(cov))
plot(x,bimodal(x,*params),color='red',lw=3,label='model')
legend()
print(params,'\n',sigma)

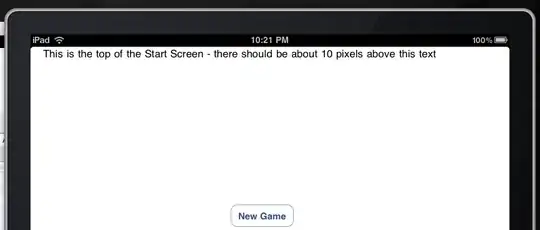
Here is the output plot:

Output plot of fitting two Gaussian Distributions within the same dataset

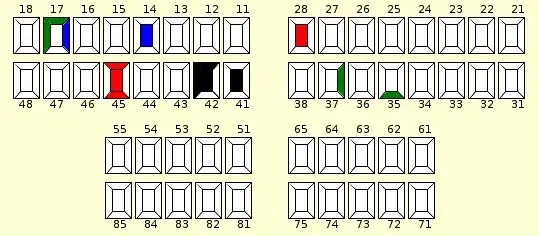
Here's the behaviour I'm expecting, a bimodal behaviour from emcee and mpfit implementation. Plot with emcee and mpfit

Any idea why that might be happening? Thanks in advance.

Edit:

Based on Mr. T's helpful suggestions, I have the following result:

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.optimize import curve_fit

np.random.seed(123)
#data=np.concatenate((np.random.normal(1, .2, 5000), np.random.normal(1.6, .3, 2500)))
data = pd.read_csv('gmm_outdata_ngc2173.csv')
gmm_3 = data['col3']
y,x,_=plt.hist(gmm_3, 22, alpha=.3, label='data')
x=(x[1:]+x[:-1])/2 # for len(x)==len(y)
#%%
def gauss(x, mu, sigma, A):
    return A*np.exp(-(x-mu)**2/2/sigma**2)

def bimodal(x, mu1, sigma1, A1, mu2, sigma2, A2):
    return gauss(x,mu1,sigma1,A1)+gauss(x,mu2,sigma2,A2)

#expected = (1, .2, 250, 2, .2, 125)
expected=(-0.15,.02,22,0.15,.02,22)
params, cov = curve_fit(bimodal, x, y, expected)
sigma=np.sqrt(np.diag(cov))
x_fit = np.linspace(x.min(), x.max(), 500)
plt.plot(x_fit, bimodal(x_fit, *params), color='red', lw=3, label='model')
plt.plot(x_fit, gauss(x_fit, *params[:3]), color='red', lw=1, ls="--", label='distribution 1')
plt.plot(x_fit, gauss(x_fit, *params[3:]), color='red', lw=1, ls=":", label='distribution 2')
plt.legend()
#print(pd.DataFrame(data={'params': params, 'sigma': sigma}, index=bimodal.__code__.co_varnames[1:]))
plt.show()

When I try to change "*params[3:]", I get an error gauss() missing 1 required positional argument: 'A'. Mr. T's code's output. Edit 2:

I am uploading the data I am working on. Please have a look here.

Hi. Thanks for your response. I have added the part of expected behaviour in my question. I want to show the bimodality which is present in the data I obtain from the Gaussian mixture modelling (gmm). The gmm code I'm using successfully detects the second peak, I only want to display two Gaussian distributions on the same data set. Please let me know if you have any ideas or suggestions. Thanks so much! — surviving-grad, Jan 29 '22 at 14:00
So, your problem is that your graph doesn't show the separate Gaussian components? I mean, your output obviously has two peaks. — Mr. T, Jan 29 '22 at 14:45
As an aside: [Don't use pylab](https://matplotlib.org/stable/api/index.html#module-pylab), [dont' use `import *`](https://stackoverflow.com/questions/2386714/why-is-import-bad). — Mr. T, Jan 29 '22 at 14:47
@Mr. T Yes, that's exactly my problem. Thanks for the tip for not using pylab and not importing *. — surviving-grad, Jan 29 '22 at 22:11
As I see quite often references to the answer you lifted your code from, I have [rewritten the code without pylab](https://stackoverflow.com/a/70907042/8881141) and added the two distributions. Just for you. — Mr. T, Jan 29 '22 at 23:33
This is exactly, what I wanted. Let me try it for my dataset, and get back to you. Thanks so much! — surviving-grad, Jan 30 '22 at 05:14
Hi, I have edited my question with my latest trials (from @Mr.T T's suggestions.). I have also uploaded the dataset I am working on. Please help. Thanks! — surviving-grad, Jan 30 '22 at 06:13

score 0 · Answer 1 · answered Jan 30 '22 at 09:04

Curve fitting is often sensitive to changes in start values. In a histogram, you get a good idea of the mean values and amplitudes of the two peaks, and we should make use of it. We should also restrict sigma values and amplitudes to nonnegative values:

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.optimize import curve_fit

data = np.genfromtxt("test.csv", skip_header=True)

y,x,_=plt.hist(data, 22, alpha=.3,label='data')
x=(x[1:]+x[:-1])/2 

def gauss(x, mu, sigma, A):
    return A*np.exp(-(x-mu)**2/2/sigma**2)

def bimodal(x, mu1, sigma1, A1, mu2, sigma2, A2):
    return gauss(x, mu1, sigma1, A1)+gauss(x, mu2, sigma2, A2)

expected = (0, .01, 20, .1, .01, 5)
params, cov = curve_fit(bimodal, x, y, expected, 
                        #[[lower], [upper]] bounds for mu1, sigma1, A1, mu2, sigma2, A2
                        bounds=[[-np.inf, 0, 0, -np.inf, 0, 0], [np.inf, np.inf, np.inf, np.inf, np.inf, np.inf]]) 
sigma=np.sqrt(np.diag(cov))
x_fit = np.linspace(x.min(), x.max(), 500)
plt.plot(x_fit, bimodal(x_fit, *params), color='red', lw=3, label='model')
plt.plot(x_fit, gauss(x_fit, *params[:3]), color='red', lw=1, ls="--", label='distribution 1')
plt.plot(x_fit, gauss(x_fit, *params[3:]), color='red', lw=1, ls=":", label='distribution 2')
plt.legend()
print(pd.DataFrame(data={'params': params, 'sigma': sigma}, index=bimodal.__code__.co_varnames[1:]))
plt.show()

Output:

           params     sigma
mu1      0.003198  0.005179
sigma1   0.042710  0.005658
A1      18.119693  1.840331
mu2      0.097203  0.009387
sigma2   0.010044  0.007779
A2       5.346416  3.519740

Plot two gaussian distributions out of the data using gaussian mixture model (not a repeated question)

1 Answers1