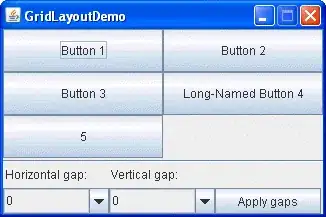
Alright so I think I got this dialed in. I wont go over the how, other than to say that once you study the code enough the black magic doesn't go away but patterns do emerge. I just extended those patterns and it looks like it works.
End result

Admittedly this is so low res that it look like its not changing from C=1 to C=2 but it is. Load it up and you'll see. The gif should show the flow more cleary now.
First the methodology behind the proof. I found a funky surface equation and added a third input variable C (in-effect creating a 4D surface), then studied the surface shape with fixed C values using the original 3D fitter/renderer as a point of trusted reference.
When C is 1, you get a half pipe from hell. A slightly lopsided downsloping halfpipe.

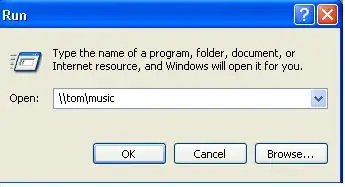
Whence C is 2, you get much the same but the lopsidedness is even more exaggerated.

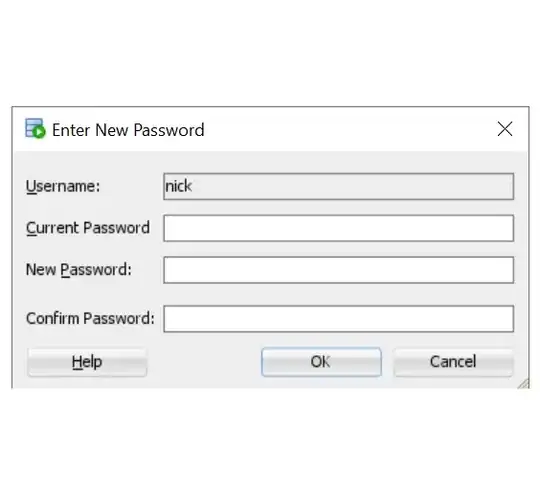
When C is 3, you get a very different shape. Like the exaggerated half pipe from above was cut in half, reversed, and glued back together.
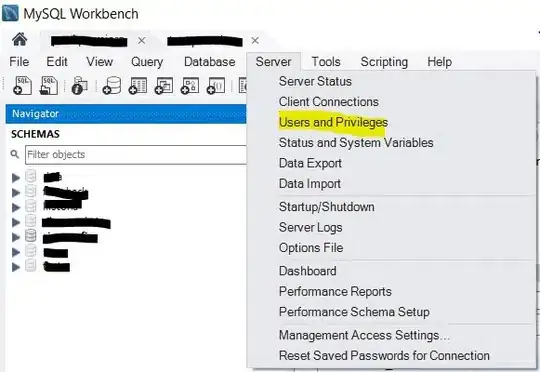
When you run the below code, you get a 3D render with a slider that allows you to flow through the C values from 1 to 3. The values at 1, 2, and 3 look like solid matches to the references. I also added a randomizer to the data to see how it would perform at approximating a surface from imperfect noisy data and I like what I see there too.
Props to the below questions for their code and ideas.
Python 3D polynomial surface fit, order dependent
python visualize 4d data with surface plot and slider for 4th variable
import itertools
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.widgets import Slider
class Surface4D:
def __init__(self, order, a, b, c, z):
# Setting initial attributes
self.order = order
self.a = a
self.b = b
self.c = c
self.z = z
# Setting surface attributes
self.surface = self._fit_surface()
self.aa = None
self.bb = None
self._sample_surface_grid()
# Setting graph attributes
self.surface_render = None
self.axis_3d = None
# Start black magic math
def _abc_powers(self):
powers = itertools.product(range(self.order + 1), range(self.order + 1), range(self.order + 1))
return [tup for tup in powers if sum(tup) <= self.order]
def _fit_surface(self):
ncols = (self.order + 1)**3
G = np.zeros((self.a.size, ncols))
ijk = self._abc_powers()
for idx, (i,j,k) in enumerate(ijk):
G[:,idx] = self.a**i * self.b**j * self.c**k
m, _, _, _ = np.linalg.lstsq(G, self.z, rcond=None)
return m
def get_z_values(self, a, b, c):
ijk = self._abc_powers()
z = np.zeros_like(a)
for s, (i,j,k) in zip(self.surface, ijk):
z += s * a**i * b**j * c**k
return z
# End black magic math
def render_4d_flow(self):
# Set up the layout of the graph
fig = plt.figure()
self.axis_3d = Axes3D(fig, rect=[0.1,0.2,0.8,0.7])
slider_ax = fig.add_axes([0.1,0.1,0.8,0.05])
self.axis_3d.set_xlabel('X data')
self.axis_3d.set_ylabel('Y data')
self.axis_3d.set_zlabel('Z data')
# Plot the point cloud and initial surface
self.axis_3d.scatter(self.a, self.b, self.z, color='red', zorder=0)
zz = self.get_z_values(self.aa, self.bb, 1)
self.surface_render = self.axis_3d.plot_surface(self.aa, self.bb, zz, zorder=10, alpha=0.4, color="b")
# Setup the slider behavior
slider_start_step = self.c.min()
slider_max_steps = self.c.max()
slider = Slider(slider_ax, 'time', slider_start_step, slider_max_steps , valinit=slider_start_step)
slider.on_changed(self._update)
plt.show()
input("Once youre done, hit any enter to continue.")
def _update(self, val):
self.surface_render.remove()
zz = self.get_z_values(self.aa, self.bb, val)
self.surface_render = self.axis_3d.plot_surface(self.aa, self.bb, zz, zorder=10, alpha=0.4, color="b")
def _sample_surface_grid(self):
na, nb = 40, 40
aa, bb = np.meshgrid(np.linspace(self.a.min(), self.a.max(), na),
np.linspace(self.b.min(), self.b.max(), nb))
self.aa = aa
self.bb = bb
def noisify_array(one_dim_array, randomness_multiplier):
listOfNewValues = []
range = abs(one_dim_array.min()-one_dim_array.max())
for item in one_dim_array:
# What percentage are we shifting the point dimension by
shift = np.random.randint(0, 101)
shiftPercent = shift/100
shiftPercent = shiftPercent * randomness_multiplier
# Is that shift positive or negative
shiftSignIndex = np.random.randint(0, 2)
shifSignOption = [-1, 1]
shiftSign = shifSignOption[shiftSignIndex]
# Shift it
newNoisyPosition = item + (range * (shiftPercent * shiftSign))
listOfNewValues.append(newNoisyPosition)
return np.array(listOfNewValues)
def generate_data():
# Define our range for each dimension
x = np.linspace(-6, 6, 20)
y = np.linspace(-6, 6, 20)
w = [1, 2, 3]
# Populate each dimension
a,b,c,z = [],[],[],[]
for X in x:
for Y in y:
for W in w:
a.append(X)
b.append(Y)
c.append(W)
z.append((1 * X ** 4) + (2 * Y ** 3) + (X * Y ** W) + (4 * X) + (5 * Y))
# Convert them to arrays
a = np.array(a)
b = np.array(b)
c = np.array(c)
z = np.array(z)
return [a, b, c, z]
def main(order):
# Make the data
a,b,c,z = generate_data()
# Show the pure data and best fit
surface_pure_data = Surface4D(order, a, b, c, z)
surface_pure_data.render_4d_flow()
# Add some noise to the data
a = noisify_array(a, 0.10)
b = noisify_array(b, 0.10)
c = noisify_array(c, 0.10)
z = noisify_array(z, 0.10)
# Show the noisy data and best fit
surface_noisy_data = Surface4D(order, a, b, c, z)
surface_noisy_data.render_4d_flow()
# ----------------------------------------------------------------
orderForSurfaceFit = 5
main(orderForSurfaceFit)
[Edit 1: I've started to incorporate this code into my real projects and I found some tweaks to make things ore sensible. Also there's a scope problem where the runtime needs to be paused while it's still in the scope of the render_4d_flow function in order for the slider to work.]
[Edit 2: Higher resolution gif that shows the flow from c=2 to c=3]