I need to calculate the following integral on a 2D-grid (x,y positions):
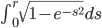
with r = sqrt(x^2 + y^2) and the 2D-grid centered at x=y=0. The implementation is straightforward:
import numpy as np
from scipy import integrate
def integralFunction(x):
def squareSaturation(y):
return np.sqrt(1-np.exp(-y**2))
return integrate.quad(squareSaturation,0,x)[0]
#vectorize function to apply function with integrals on np-array
integralFunctionVec = np.vectorize(integralFunction)
xmax = ymax = 5
Nx = Ny = 1024
X, Y = np.linspace(-xmax, xmax, Nx), np.linspace(-ymax, ymax, Ny)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2+Y**2)
Z = integralFunctionVec(R)
However, I'm currently working on a 1024x1024 grid and the calculation takes ~1.5 minutes. Now there is some redundancy in those calculations that I want to reduce to speed up the calculation. Namely:
As the grid is centered around r = 0, many values for r on the grid are the same. Due to symmetry only ~1/8 of all values are unique (for a square grid). One idea was to calculate the integral only for the unique values (found via np.unique) and then save them in a look-up table (hashmap?) Or I could cache the function values so that only new values are calculated (via @lru_cache). But does that actually work when I vectorize the function afterwards?
As the integral goes from 0 to r, the integral is often calculating integrals over intervals it has already calculated. E.g. if you calculate from 0 to 1 and afterwards from 0 to 2, only the interval from 1 to 2 is "new". But what would be the best way to utilize that? And would that even be a real performance boost using scipy.integrate.quad?
Do you have any feedback or other ideas to optimize this calculation?