Transform a coordinate sytem into a Matrix in Mathematica

Question

Ahead of a the programming question, I believe I need to give a little background of what I am doing to ease the understanding of my problem :

I record eye-movements while displaying some patterns to subjects subject. Through the experiment, I later display some symmetrical transform of those patterns.

What I get is lists of fixations coordinates and durations :

{{fix1X,fix1Y,fix1Dn},{fix2X,fix2Y,fix2Dn},...{fixNX,fixNY,fixNDn}}

Where :

-fix1X is the X coordinate for the first fixation.

-fix1Y is the Y coordinate for the first fixation.

-fix1D is the duration in milliseconds of the fixations

Please consider :

FrameWidth  = 31.36;
scrHeightCM = 30;
scrWidthCM  = 40;
FrameXYs    = {{4.32, 3.23}, {35.68, 26.75}};  (* {{Xmin,Ymin},{Xmax,Ymax}} *)

Below are the fixations for 1 Display (Subject Fixations during the 3s stimuli presentation on the screen)

fix ={{20.14, 15.22, 774.}, {20.26, 15.37, 518.}, {25.65, 16.22, 200.}, 
      {28.15, 11.06, 176.}, {25.25, 13.38, 154.}, {24.78, 15.74, 161.}, 
      {24.23, 16.58, 121.}, {20.06, 13.22, 124.}, {24.91, 15.8, 273.}, 
      {24.32, 12.83, 119.}, {20.06, 12.14, 366.}, {25.64, 18.22, 236.}, 
      {24.37, 19.2, 177.}, {21.02, 16.4, 217.}, {20.63, 15.75,406.}}

Graphics[{
          Gray, EdgeForm[Thick],
          Rectangle @@ {{0, 0}, {scrWidthCM, scrHeightCM}},
          White,
          Rectangle @@ StimuliFrameCoordinates,
          Dashed, Black,
         Line[
             {{(scrWidthCM/2), FrameXYs[[1, 2]]},
             {(scrWidthCM/2), FrameXYs[[2, 2]]}}],
         Line[
             {{FrameXYs[[1, 1]], (scrHeightCM/2)},
             {(FrameXYs[[2, 1]]), (scrHeightCM/2)}}],

         Thickness[0.005], Pink,
         Disk[{#[[1]], #[[2]]}, 9 N[#[[3]]/Total[fix[[All, 3]]]]] & /@ fix
         }, ImageSize -> 500]

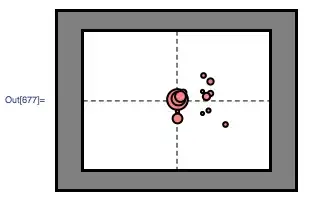
What I want to do :

I would like to "discretize" the stimuli frame space into clusters :

Below is a visual representation (done in PPT) with different clusters (2,4,16,64).

The colored part representing the clusters in which fixations occurred :

With this I want to

-Count the number of fixations within each cluster.

-Compute the presence/count or duration observed in each cluster.

A Matrix form would easily enable me to compare different displays fixations by subtraction.

So, question(s)

-How can I create a flexible mechanism to divide the stimuli frame into clusters.

-Map the fixations onto those clusters obtaining a rectangular Matrix filled with 0s or fixations counts or total fixations duration for each of the matrix cell.

I feel this question could be unclear and will edit it to clarify anything needed. Also, would you think this should be asked in 2 separate questions, I am happy to do so.

Many thank in advance for any help you could provide.

Answer 1

You can do something like:

createMatrix[list_, frameXYs_, partitX_, partitY_, fun_] :=
 Module[{matrix},
  (*init return matrix*)
  matrix = Array[0 &, {partitX, partitY}];
  (matrix[[
    IntegerPart@Rescale[#[[1]], {frameXYs[[1, 1]], frameXYs[[2, 1]]}, {1,partitX}],
    IntegerPart@Rescale[#[[2]], {frameXYs[[1, 2]], frameXYs[[2, 2]]}, {1,partitY}]
         ]] += fun[#[[3]]]) & /@ list;

  Return@(matrix[[1 ;; -2, 1 ;; -2]]);]

Where fun is the counting function on the third dimension of your list.

So, if you want to count occurrences:

fix = {{20.14, 15.22, 774.}, {20.26, 15.37, 518.}, {25.65, 16.22, 200.}, 
       {28.15, 11.06, 176.}, {25.25, 13.38, 154.}, {24.78, 15.74, 161.}, 
       {24.23, 16.58, 121.}, {20.06, 13.22, 124.}, {24.91, 15.8,  273.}, 
       {24.32, 12.83, 119.}, {20.06, 12.14, 366.}, {25.64, 18.22, 236.}, 
       {24.37, 19.2, 177.},  {21.02, 16.4, 217.},  {20.63, 15.75, 406.}};
FrameXYs = {{4.32, 3.23}, {35.68, 26.75}};

cm = createMatrix[fix, FrameXYs, 10, 10, 1 &]
MatrixPlot@cm
MatrixForm@cm

And if you want to add up fixation time

cm = createMatrix[fix, FrameXYs, 10, 10, # &]
MatrixPlot@cm
MatrixForm@cm

Edit

Making some adjustments in the indexes, a little code embellishment, an a clearer example:

createMatrix[list_, frameXYs_, partit : {partitX_, partitY_}, fun_] :=
 Module[{matrix, g},
  (*Define rescale function*)
  g[i_, l_] := IntegerPart@
                   Rescale[l[[i]], (Transpose@frameXYs)[[i]], {1, partit[[i]]}];
  (*Init return matrix*)
  matrix = Array[0 &, {partitX + 1, partitY + 1}];
  (matrix[[g[1, #], g[2, #]]] += fun[#[[3]]]) & /@ list;
  Return@(matrix[[1 ;; -2, 1 ;; -2]]);]

.

fix = {{1, 1, 1}, {1, 3, 2}, {3, 1, 3}, {3, 3, 4}, {2, 2, 10}};
FrameXYs = {{1, 1}, {3, 3}};
cm = createMatrix[fix, FrameXYs, {7, 7}, # &];
MatrixPlot@cm
Print[MatrixForm@SparseArray[(#[[1 ;; 2]] -> #[[3]]) & /@ fix], MatrixForm@cm]

Answer 2

There are a couple of things that have to be done to accomplish what you want. First, given a division count we have to divide up the 2-dimensional space. Second, using the division count, we need a flexible method of grouping the fixations into their appropriate spots. Lastly, we generate whatever statistics you need.

As to the division count, the built-in function FactorInteger almost does what you need. For example,

(* The second parameter is the upper limit for the number of factors returned *)
FactorInteger[35,2] == {{5,1}, {7,1}}
FactorInteger[64,2] == {{2,6}}

Unfortunately, you can only specify an upper limit to the number of factors returned, so we must modify the output slightly

Clear[divisionCount]
divisionCount[c_Integer?(Positive[#] && (# == 2 || ! PrimeQ[#]) &)] :=
With[{res = FactorInteger[c, 2]},
 Power @@@ If[ 
     Length[res] == 2, 
     res // Reverse,
     With[
       {q = Quotient[res[[1, 2]], 2], r = Mod[res[[1, 2]], 2], 
        b = res[[1, 1]]},
       {{b, q + r}, {b, q}}
     ]
 ]
] 

This does two things, replaces {{b,m}} with {{b, m / 2 + m mod 2}, {b, m / 2}} where / represents integer division (i.e. there are remainders) and converts {{b, m} ..} to {b^m ..} via Power @@@. This gives

divisionCount[32] == {8, 4}
divisionCount[64] == {8, 8}.

It turns out, we can get a fixation count at this point with minimal additional work via BinCounts, as follows

BinCounts[fix[[All,;;2]], (* stripping duration from tuples *)
  {xmin, xmax, (xmax - xmin)/#1,
  {ymin, ymax, (ymax - ymin)/#2]& @@ divisionCount[ divs ]

where you need to supply the ranges for x and y and the number of divisions. However, this isn't as flexible as it could be. Instead, we'll make use of SelectEquivalents.

The key to using SelectEquivalents effectively is creating a good categorization function. To do that, we need to determine the divisions ourselves, as follows

Clear[makeDivisions]
makeDivisions[
 {xmin_, xmax_, xdivs_Integer?Positive}, {ymin_, ymax_, ydivs_Integer?Positive}] :=
   Partition[#,2,1]& /@ {
     (xmax - xmin)*Range[0, xdivs]/xdivs + xmin,
     (ymax - ymin)*Range[0, ydivs]/ydivs + ymin
   }

makeDivisions[
       {xmin_, xmax_}, {ymin_, ymax_}, 
       divs_Integer?(Positive[#] && (# == 2 || ! PrimeQ[#]) &)] :=
 makeDivisions[{xmin, xmax, #1}, {ymin, ymax, #2}] & @@ divisionCount[divs]

where

makeDivisions[{0, 1}, {0, 1}, 6] == 
 {{{0, 1/3}, {1/3, 2/3}, {2/3, 1}}, {{0, 1/2}, {1/2, 1}}}.

(I would have used FindDivisions, but it doesn't always return the number of divisions you request.) makeDivisions returns two lists where each term in each list is a min-max pair that we can use to determine if a point falls into the bin.

Since we are on a square lattice, we need to test all pairs of limits that we just determined. I'd use the following

Clear[inBinQ, categorize]
inBinQ[{xmin_,xmax_}, {ymin_, ymax_}, {x_,y_}]:= 
   (xmin <= x < xmax) && (ymin <= y < ymax)

categorize[{xmin_, xmax_}, {ymin_, ymax_}, divs_][val : {x_, y_, t_}] := 
 With[{bins = makeDivisions[{xmin, xmax}, {ymin, ymax}, divs]}, 
  Outer[inBinQ[#1, #2, {x, y}] &, bins[[1]], bins[[2]], 1]] //Transpose

which returns

categorize[{0,1},{0,1},6][{0.1, 0.2, 5}] ==
 {{True, False, False}, {False, False, False}}.

Note, the y-coordinate is reversed compared to the plot, low values are at the beginning of the array. To "fix" this, Reverse bins[[2]] in categorize. Also, you'll want to remove the Transpose prior to supplying the results to MatrixPlot as it expects the results in an untransposed form.

Using

SelectEquivalents[ 
 fix, 
 (categorize[{xmin, xmax}, {ymin, ymax}, 6][#] /. {True -> 1, False -> 0} &), 
 #[[3]] &, (* strip off all but the timing data *)
{#1, #2} &],

we get

{{
  {{0, 0, 0}, {0, 1, 0}}, {774., 518., 161., 121., 273., 177., 217., 406.}
 }, 
 {
  {{0, 0, 0}, {0, 0, 1}}, {200., 236.}
 }, 
 {
  {{0, 0, 1}, {0, 0, 0}}, {176., 154.}
 }, 
 {
  {{0, 1, 0}, {0, 0, 0}}, {124., 119., 366.}
 }}}

where the first term in each sublist is a matrix representation of the bin and the second term is a list of points that fall in that bin. To determine how many are in each bin,

Plus @@ (Times @@@ ({#1, Length[#2]} & @@@ %)) ==
 {{0, 3, 2}, {0, 8, 2}}

Or, timings

Plus @@ (Times @@@ ({#1, Total[#2]} & @@@ %)) ==
 {{0, 609., 330.}, {0, 2647., 436.}}

Edit: As you can see, to get whatever statistics you need on the fixations, you just have to replace either Length or Total. For instance, you could want the average (Mean) time spent, not just the total.

Answer 3

Depending on the calculations you are performing, and the precision of the data, you may care for a softer approach. Consider using image resampling for this. Here is one possible approach. There is obvious fuzziness here, but again, that may be desirable.

fix = {{20.14, 15.22, 774.}, {20.26, 15.37, 518.}, {25.65, 16.22, 
    200.}, {28.15, 11.06, 176.}, {25.25, 13.38, 154.}, {24.78, 15.74, 
    161.}, {24.23, 16.58, 121.}, {20.06, 13.22, 124.}, {24.91, 15.8, 
    273.}, {24.32, 12.83, 119.}, {20.06, 12.14, 366.}, {25.64, 18.22, 
    236.}, {24.37, 19.2, 177.}, {21.02, 16.4, 217.}, {20.63, 15.75, 
    406.}};
FrameXYs = {{4.32, 3.23}, {35.68, 26.75}};

Graphics[{AbsolutePointSize@Sqrt@#3, Point[{#, #2}]} & @@@ fix, 
 BaseStyle -> Opacity[0.3], PlotRange -> Transpose@FrameXYs,
 PlotRangePadding -> None, ImageSize -> {400, 400}]

ImageResize[%, {16, 16}];

Show[ImageAdjust@%, ImageSize -> {400, 400}]

---

As the above is apparently unhelpful, here is an attempt to be constructive. This is my take on belisarius' fine solution. I feel that it is a little cleaner.

createMatrix[list_, {{x1_, y1_}, {x2_, y2_}}, par:{pX_, pY_}, fun_] :=
 Module[{matrix, quant},
    matrix = 0 ~ConstantArray~ par;
    quant = IntegerPart@Rescale@## &;
    (matrix[[
         quant[#1, {x1, x2}, {1, pX}],
         quant[#2, {y1, y2}, {1, pY}]
           ]] += fun[#3] &) @@@ list;
    Drop[matrix, -1, -1]
 ]

Notice that the syntax is slightly different: quantize partitions x and y are given in a list. I feel this is more consistent with other functions, such as Array.