Java rounding up to an int using Math.ceil

Question

int total = (int) Math.ceil(157/32);

Why does it still return 4? 157/32 = 4.90625, I need to round up, I've looked around and this seems to be the right method.

I tried total as double type, but get 4.0.

What am I doing wrong?

Answer 1

You are doing 157/32 which is dividing two integers with each other, which always result in a rounded down integer. Therefore the (int) Math.ceil(...) isn't doing anything. There are three possible solutions to achieve what you want. I recommend using either option 1 or option 2. Please do NOT use option 0.

Option 0

Convert a and b to a double, and you can use the division and Math.ceil as you wanted it to work. However I strongly discourage the use of this approach, because double division can be imprecise. To read more about imprecision of doubles see this question.

int n = (int) Math.ceil((double) a / b));

Option 1

int n = a / b + ((a % b == 0) ? 0 : 1); 

You do a / b with always floor if a and b are both integers. Then you have an inline if-statement which checks whether or not you should ceil instead of floor. So +1 or +0, if there is a remainder with the division you need +1. a % b == 0 checks for the remainder.

Option 2

This option is very short, but maybe for some less intuitive. I think this less intuitive approach would be faster than the double division and comparison approach:
Please note that this doesn't work for b < 0.

int n = (a + b - 1) / b;

To reduce the chance of overflow you could use the following. However please note that it doesn't work for a = 0 and b < 1.

int n = (a - 1) / b + 1;

Explanation behind the "less intuitive approach"

Since dividing two integers in Java (and most other programming languages) will always floor the result. So:

int a, b;
int result = a/b (is the same as floor(a/b) )

But we don't want floor(a/b), but ceil(a/b), and using the definitions and plots from Wikipedia:

With these plots of the floor and ceil functions, you can see the relationship.

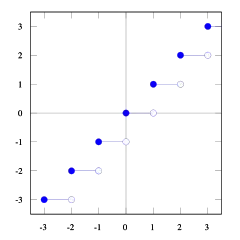
You can see that floor(x) <= ceil(x). We need floor(x + s) = ceil(x). So we need to find s. If we take 1/2 <= s < 1 it will be just right (try some numbers and you will see it does, I find it hard myself to prove this). And 1/2 <= (b-1) / b < 1, so

ceil(a/b) = floor(a/b + s)
          = floor(a/b + (b-1)/b)
          = floor( (a+b-1)/b) )

This is not a real proof, but I hope you're satisfied with it. If someone can explain it better I would appreciate it too. Maybe ask it on MathOverflow.

Answer 2

157/32 is int/int, which results in an int.

Try using the double literal - 157/32d, which is int/double, which results in a double.

Answer 3

157/32 is an integer division because all numerical literals are integers unless otherwise specified with a suffix (d for double l for long)

the division is rounded down (to 4) before it is converted to a double (4.0) which is then rounded up (to 4.0)

if you use a variables you can avoid that

double a1=157;
double a2=32;
int total = (int) Math.ceil(a1/a2);

Answer 4

int total = (int) Math.ceil((double)157/32);

Answer 5

Nobody has mentioned the most intuitive:

int x = (int) Math.round(Math.ceil((double) 157 / 32));

This solution fixes the double division imprecision.

Answer 6

In Java adding a .0 will make it a double...

int total = (int) Math.ceil(157.0 / 32.0);

Answer 7

When dividing two integers, e.g.,

int c = (int) a / (int) b;

the result is an int, the value of which is a divided by b, rounded toward zero. Because the result is already rounded, ceil() doesn't do anything. Note that this rounding is not the same as floor(), which rounds towards negative infinity. So, 3/2 equals 1 (and floor(1.5) equals 1.0, but (-3)/2 equals -1 (but floor(-1.5) equals -2.0).

This is significant because if a/b were always the same as floor(a / (double) b), then you could just implement ceil() of a/b as -( (-a) / b).

The suggestion of getting ceil(a/b) from

int n = (a + b - 1) / b;, which is equivalent to a / b + (b - 1) / b, or (a - 1) / b + 1

works because ceil(a/b) is always one greater than floor(a/b), except when a/b is a whole number. So, you want to bump it to (or past) the next whole number, unless a/b is a whole number. Adding 1 - 1 / b will do this. For whole numbers, it won't quite push them up to the next whole number. For everything else, it will.

Yikes. Hopefully that makes sense. I'm sure there's a more mathematically elegant way to explain it.

Answer 8

Also to convert a number from integer to real number you can add a dot:

int total = (int) Math.ceil(157/32.);

And the result of (157/32.) will be real too. ;)

Answer 9

int total = (int) Math.ceil( (double)157/ (double) 32);

Answer 10

Check the solution below for your question:

int total = (int) Math.ceil(157/32);

Here you should multiply Numerator with 1.0, then it will give your answer.

int total = (int) Math.ceil(157*1.0/32);

Answer 11

Use double to cast like

Math.ceil((double)value) or like

Math.ceil((double)value1/(double)value2);

Answer 12

Java provides only floor division / by default. But we can write ceiling in terms of floor. Let's see:

Any integer y can be written with the form y == q*k+r. According to the definition of floor division (here floor) which rounds off r,

floor(q*k+r, k) == q  , where 0 ≤ r ≤ k-1

and of ceiling division (here ceil) which rounds up r₁,

ceil(q*k+r₁, k) == q+1  , where 1 ≤ r₁ ≤ k

where we can substitute r+1 for r₁:

ceil(q*k+r+1, k) == q+1  , where 0 ≤ r ≤ k-1

Then we substitute the first equation into the third for q getting

ceil(q*k+r+1, k) == floor(q*k+r, k) + 1  , where 0 ≤ r ≤ k-1

Finally, given any integer y where y = q*k+r+1 for some q,k,r, we have

ceil(y, k) == floor(y-1, k) + 1

And we are done. Hope this helps.

Answer 13

There are two methods by which you can round up your double value.

1. Math.ceil
2. Math.floor

If you want your answer 4.90625 as 4 then you should use Math.floor and if you want your answer 4.90625 as 5 then you can use Math.ceil

You can refer following code for that.

public class TestClass {

    public static void main(String[] args) {
        int floorValue = (int) Math.floor((double)157 / 32);
        int ceilValue = (int) Math.ceil((double)157 / 32);
        System.out.println("Floor: "+floorValue);
        System.out.println("Ceil: "+ceilValue);

    }

}

Answer 14

I know this is an old question but in my opinion, we have a better approach which is using BigDecimal to avoid precision loss. By the way, using this solution we have the possibility to use several rounding and scale strategies.

final var dividend = BigDecimal.valueOf(157);
final var divisor = BigDecimal.valueOf(32);
final var result = dividend.divide(divisor, RoundingMode.CEILING).intValue();

Answer 15

int total = (157-1)/32 + 1

or more general

(a-1)/b +1