Shortest path in an unweighted graph like this is typically best done with a breadth-first search, which is implemented iteratively using a queue data structure to store search state, rather than a depth-first search using a stack (such as the call stack and recursion).
If you use a stack, a search that happens to hit the goal node isn't necessarily shortest, because the path isn't extended methodically one level at a time as in BFS. Rather, the DFS explores all the way to a terminal state as soon as possible, then begins to backtrack and explore other terminal paths. None of these paths have the shortness guarantee of BFS.
The consequence of this is that with a naive recursive implementation, you will need to explore all paths before you can claim you've found the shortest one. But if your grids are small or have few paths as appears to be the case here, this shouldn't be a problem.
If you do need to optimize yet maintain the recursion, see the canonical thread Performing Breadth First Search recursively. But going forward I'll assume we're doing DFS.
The other concern is that when the graph has cycles, you need to be able to keep track of visited nodes to avoid an infinite loop. Since you seem to not mind changing characters in your grid, it should suffice that you'll never try to re-visit a cell marked '-' and you'll undo any '-' mark at the end of a recursive call in case you find a faster path to that cell in the future.
As a C-specific aside, it's best not to write function headers like char fun(char arr[][3]). The name is unclear, as is the return value, and the parameter is hard-coded to be exactly 3 columns wide. It's unrealistic to expect a client calling the function from a library to go in and edit the source code every time they want to use a different grid. Even if they did, they'd be prohibited from calling this function on multiple grid sizes in the same program. That size should be dynamic. Also, the function relies on global state, int startRow = 0, startColumn = 0; which is not thread-safe and very prone to errors. Pass all state as parameters, or at least only read global constants.
Here's a proof of concept that could still use some clean-up (repeated code, hardcoded literals). Basically, run a standard DFS to get the length of the shortest path, then run it again to populate the first path that fulfills the minimum length requirement: very much a brute-force approach.
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void ensure(bool predicate, const char *msg, unsigned int line) {
if (!predicate) {
fprintf(stderr, "%s:%d: %s\n", __FILE__, line, msg);
exit(1);
}
}
void print_grid(size_t rows, size_t cols, char **grid) {
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
printf("%c", grid[i][j]);
}
puts("");
}
}
void find_shortest_path_recursive(
int path_length,
int *shortest_path_length,
int y,
int x,
size_t rows,
size_t cols,
char **grid
) {
if (y < 0 || x < 0 || y >= rows ||
x >= cols || grid[y][x] != '1') {
return;
}
else if (y == rows - 1 && x == cols - 1 &&
(*shortest_path_length < 0 ||
path_length < *shortest_path_length)) {
*shortest_path_length = path_length + 1;
}
grid[y][x] = '-';
const static int dirs[][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
for (int i = 0; i < 4; i++) {
find_shortest_path_recursive(
path_length + 1,
shortest_path_length,
y + dirs[i][0],
x + dirs[i][1],
rows,
cols,
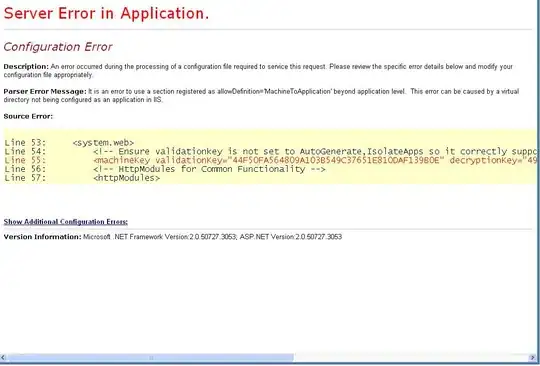
grid
);
}
grid[y][x] = '1';
}
bool set_shortest_path_recursive(
int path_length,
int shortest_path_length,
int y,
int x,
size_t rows,
size_t cols,
char **grid
) {
if (y < 0 || x < 0 || y >= rows ||
x >= cols || grid[y][x] != '1') {
return false;
}
grid[y][x] = '-';
if (y == rows - 1 && x == cols - 1 &&
path_length + 1 == shortest_path_length) {
return true;
}
const static int dirs[][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
for (int i = 0; i < 4; i++) {
if (set_shortest_path_recursive(
path_length + 1,
shortest_path_length,
y + dirs[i][0],
x + dirs[i][1],
rows,
cols,
grid
)) {
return true;
}
}
grid[y][x] = '1';
return false;
}
int set_shortest_path(size_t rows, size_t cols, char **grid) {
int shortest_path_length = -1;
find_shortest_path_recursive(
0, &shortest_path_length, 0, 0, rows, cols, grid
);
set_shortest_path_recursive(
0, shortest_path_length, 0, 0, rows, cols, grid
);
return shortest_path_length;
}
int main(void) {
size_t rows = 8;
size_t cols = 8;
char src_grid[8][8] = {
"10011110",
"10001011",
"11111010",
"00100010",
"00110110",
"11100010",
"10011110",
"11110011",
};
char **grid = malloc(sizeof(*grid) * rows);
ensure(grid, "malloc failed", __LINE__);
for (int i = 0; i < rows; i++) {
grid[i] = malloc(sizeof(grid[i]) * cols);
ensure(grid[i], "malloc failed", __LINE__);
memcpy(grid[i], src_grid[i], cols);
}
int shortest_path_length = set_shortest_path(rows, cols, grid);
print_grid(rows, cols, grid);
printf("shortest path length: %d\n", shortest_path_length);
return 0;
}
Output:
-001---0
-000-0-1
-----0-0
001000-0
001101-0
111000-0
100111-0
111100--
shortest path length: 19