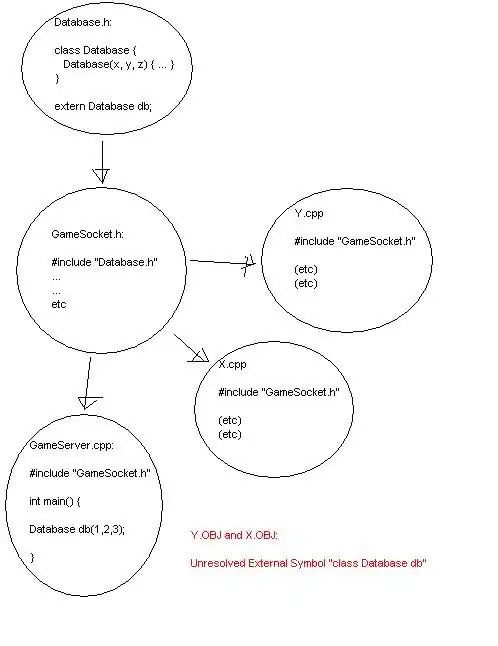
You have just single ugly slice because I do not see any z in your code (its correct the surface has horizontal and vertical sin waves like this every 0.5*pi in z).
To see the 3D surface you have to raycast z ...
I would expect some conditional testing of actually iterated x,y,z result of gyroid equation against some small non zero number like if (result<= 1e-6) and draw the stuff only then or compute color from the result instead. This is ideal to do in GLSL.
In case you are not familiar with GLSL and shaders the Fragment shader is executed for each pixel (called fragment) of the rendered QUAD so you just put the code inside your nested x,y for loops and use your x,y instead of pos (you can ignore the Vertex shader its not important).
You got 2 basic options to render this:
Blending the ray casted surface pixels together creating X-Ray like image. It can be combined with SSS techniques to get the impression of glass or semitransparent material. Here simple GLSL example for the blending:
Vertex:
#version 400 core
in vec2 position;
out vec2 pos;
void main(void)
{
pos=position;
gl_Position = vec4(position.xy,0.0,1.0);
}
Fragment:
#version 400 core
in vec2 pos;
out vec3 out_col;
void main(void)
{
float n,x,y,z,dz,d,i,di;
const float scale=2.0*3.1415926535897932384626433832795;
n=100.0; // layers
x=pos.x*scale; // x postion of pixel
y=pos.y*scale; // y postion of pixel
dz=2.0*scale/n; // z step
di=1.0/n; // color increment
i=0.0; // color intensity
for (z=-scale;z<=scale;z+=dz) // do all layers
{
d =sin(x)*cos(y); // compute gyroid equation
d+=sin(y)*cos(z);
d+=sin(z)*cos(x);
if (d<=1e-6) i+=di; // if near surface add to color
}
out_col=vec3(1.0,1.0,1.0)*i;
}
Usage is simple just render 2D quad covering screen without any matrices with corner pos points in range <-1,+1>. Here result:
Another technique is to render first hit to surface creating mesh like image. In order to see the details we need to add basic (double sided) directional lighting for which surface normal is needed. The normal can be computed by simply partialy derivate the equation by x,y,z. As now the surface is opaque then we can stop on first hit and also ray cast just single period in z as anything after that is hidden anyway. Here simple example:
Fragment:
#version 400 core
in vec2 pos; // input fragmen (pixel) position <-1,+1>
out vec3 col; // output fragment (pixel) RGB color <0,1>
void main(void)
{
bool _discard=true;
float N,x,y,z,dz,d,i;
vec3 n,l;
const float pi=3.1415926535897932384626433832795;
const float scale =3.0*pi; // 3.0 periods in x,y
const float scalez=2.0*pi; // 1.0 period in z
N=200.0; // layers per z (quality)
x=pos.x*scale; // <-1,+1> -> [rad]
y=pos.y*scale; // <-1,+1> -> [rad]
dz=2.0*scalez/N; // z step
l=vec3(0.0,0.0,1.0); // light unit direction
i=0.0; // starting color intensity
n=vec3(0.0,0.0,1.0); // starting normal only to get rid o warning
for (z=0.0;z>=-scalez;z-=dz) // raycast z through all layers in view direction
{
// gyroid equation
d =sin(x)*cos(y); // compute gyroid equation
d+=sin(y)*cos(z);
d+=sin(z)*cos(x);
// surface hit test
if (d>1e-6) continue; // skip if too far from surface
_discard=false; // remember that surface was hit
// compute normal
n.x =+cos(x)*cos(y); // partial derivate by x
n.x+=+sin(y)*cos(z);
n.x+=-sin(z)*sin(x);
n.y =-sin(x)*sin(y); // partial derivate by y
n.y+=+cos(y)*cos(z);
n.y+=+sin(z)*cos(x);
n.z =+sin(x)*cos(y); // partial derivate by z
n.z+=-sin(y)*sin(z);
n.z+=+cos(z)*cos(x);
break; // stop raycasting
}
// skip rendering if no hit with surface (hole)
if (_discard) discard;
// directional lighting
n=normalize(n);
i=abs(dot(l,n));
// ambient + directional lighting
i=0.3+(0.7*i);
// output fragment (render pixel)
gl_FragDepth=z; // depth (optional)
col=vec3(1.0,1.0,1.0)*i; // color
}
I hope I did not make error in partial derivates. Here result:

[Edit1]
Based on your code I see it like this (X-Ray like Blending)
var mat = EmguExtensions.InitMat(new System.Drawing.Size(2000, 1080));
double zz, dz, d, i, di = 0;
const double scalex = 2.0 * Math.PI / mat.Width;
const double scaley = 2.0 * Math.PI / mat.Height;
const double scalez = 2.0 * Math.PI;
uint layerCount = 100; // layers
for (int y = 0; y < mat.Height; y++)
{
double yy = y * scaley; // y position of pixel
for (int x = 0; x < mat.Width; x++)
{
double xx = x * scalex; // x position of pixel
dz = 2.0 * scalez / layerCount; // z step
di = 1.0 / layerCount; // color increment
i = 0.0; // color intensity
for (zz = -scalez; zz <= scalez; zz += dz) // do all layers
{
d = Math.Sin(xx) * Math.Cos(yy); // compute gyroid equation
d += Math.Sin(yy) * Math.Cos(zz);
d += Math.Sin(zz) * Math.Cos(xx);
if (d > 1e-6) continue;
i += di; // if near surface add to color
}
i*=255.0;
mat.SetByte(x, y, (byte)(i));
}
}