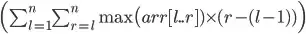Sum of the maximums of all subarrays multiplied by their lengths, in linear time

Question

Given an array I should compute the following sum in linear time:

My most naive implementation is O(n³):

sum_ = 0

for i in range(n):
    for j in range(n, i, -1):
        sum_ += max(arr[i:j]) * (j-i)

I have no idea what to do. I have tried many algorithms but they were at best O(n*log(n)), but I should solve it in linear time. Also, I don't get the idea, is there a mathematical way of just looking at an array and telling the result of the above sum?

_"I should solve it in linear time"_. Even before looking at the problem, the first question is, are you sure this can be solved in linear time? — Abhinav Mathur, Apr 04 '22 at 04:26
@AbhinavMathur thanks for your point, this problem was given to me by my cs professor so I am pretty sure it is solvable although I might be wrong in that case the professor is wrong which is not likely. — Hamed_Gholami, Apr 04 '22 at 04:31
@Hamed the professor might want you to analyse all options and provide a comprehensive proof of why `O(n)` _isn't_ possible — Abhinav Mathur, Apr 04 '22 at 04:33
@AbhyudayVaish my university's official language is not English so I don't think I can give a direct useful link. — Hamed_Gholami, Apr 04 '22 at 04:33
@AbhinavMathur no it is not like that, this is a problem that we should write a code for, and if it is not fast enough it would fail the test cases. everyone should write their program in python so everyone is equally judged. — Hamed_Gholami, Apr 04 '22 at 04:35
This can be solved in linear time; it's very similar to many other subarray problems, such as [this one](https://stackoverflow.com/questions/70293944/find-the-sum-of-maximum-difference-of-all-possible-subarrays), which can also be solved in linear time. — kcsquared, Apr 04 '22 at 04:52
If you know and have saved the sum of the last `t` elements, the sum of the last `t+1` elements requires adding a single value to that sum--hence, linear time. — Cary Swoveland, Apr 04 '22 at 04:58
@kcsquared I am sorry to bother you again but in your algorithm, we get the sum of maximums directly but I need to multiply each max by the length of the subarray, is there any solution to do that in your algorithm or should I get the index of the previous_largest and next_larger_or_equal and then do the weighting myself? thanks again. — Hamed_Gholami, Apr 04 '22 at 11:14
@CarySwoveland Even after solving this, I don't see how you mean that. Can you please show it? — Kelly Bundy, Apr 04 '22 at 18:01
@Kelly, sorry, I meant "maximum" where I said "sum". Suppose the array were `a = [5, 3, 4, 2]`. Then in linear time we can produce the array/list `mx = [5, 4, 4, 2]`, where `2` is the last element of `a`, the second `4` is the maximum of the last two elements, `[4,2].max #=> 4`, the first `4` is the maximum of the last three elements, `[4,4].max #=> 4` and `5` is the maximum of the last four elements (all elements), `[5,4].max #=> 5`. The sums of the products of this array and the terms `r - (l-1)` is then another linear time calculation; hence, the entire calculation is linear in time... — Cary Swoveland, Apr 05 '22 at 08:07
@CarySwoveland Ok, now the linear maxing is clear. But the part with "the terms r - (l-1)" is still unclear, as there are quadratically many of those terms, not linear. (Btw I know the question is tagged Python, but I think I'm not the only one who wouldn't mind seeing a Ruby implementation of your algorithm :-) — Kelly Bundy, Apr 05 '22 at 08:23

Kelly Bundy · Accepted Answer · 2022-04-08T18:35:13.710

Keep a stack of (indices of) non-increasing values. So before appending the new value, pop smaller ones. Whenever you pop one, add its contribution to the total.

def solution(arr):
    arr.append(float('inf'))
    I = [-1]
    total = 0
    for i in range(len(arr)):
        while arr[i] > arr[I[-1]]:
            j = I.pop()
            a = j - I[-1]
            b = i - j
            total += (a+b)*a*b//2 * arr[j]
        I.append(i)
    arr.pop()
    return total

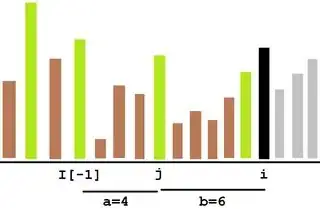
The bars represent values, larger values are larger bars. The value at i is about to be added. The light grey ones come later. The green ones are on the stack. The brown ones already don't play a role anymore. First the one at i-1 gets popped, but that's less informative. Then the one at j gets popped. It dominates the range between I[-1] and i: it's the maximum in all subarrays in that range that contain it. These subarrays contain j as well as 0 to a-1 more elements to the left and 0 to b-1 more elements to the right. That's a*b subarrays and their average length is (a+b)/2.

I temporarily append infinity to the values so it works as a sentinel on the left (avoids an extra check in the while condition) and as a cleaner at the end (it causes all remaining values to get popped from the stack). Non-Python-coders: Python supports negative indexes, -1 means "last element" (1st from the end).

Correctness test with random lists of 500 values (Try it online!):

import random

def reference(arr):
    n = len(arr)
    return sum(max(arr[L : R+1]) * (R - (L-1))
               for L in range(n)
               for R in range(L, n))

for _ in range(5):
    arr = random.choices(range(10000), k=500)
    expect = reference(arr)
    result = solution(arr)
    print(result == expect, result)

Sample output (results for five lists, True means it's correct):

True 207276773131
True 208127393653
True 208653950227
True 208073567605
True 206924015682

you are completely right, thanks. One last question though, If I want to learn to be able to solve this kind of question myself, is there anything you suggest? like any course, book, site, or exercise? — Hamed_Gholami, Apr 04 '22 at 18:01
I'd say sites like LeetCode, which have many such problems and where you can see and learn from other people's solutions. — Kelly Bundy, Apr 04 '22 at 18:04
This is brilliant; the formula `(a+b)*a*b//2` for average lengths of subarrays times the number of subarrays is a very nice touch. — kcsquared, Apr 04 '22 at 20:14

Sum of the maximums of all subarrays multiplied by their lengths, in linear time

1 Answers1