Find all nodes that are a leaf in a graph

Question

I have a function that determines if a node is a leaf.

I define a leaf as being a node that is not part of a cycle in the graph.

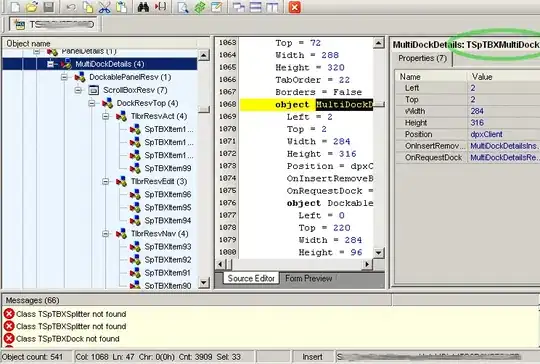
An example:

Leaf nodes are marked with red arrows, they do not belong to a cycle.

Before I find all the cycles in the graph, I first want to eliminate the need to check these leaf nodes to optimise my algorithm.

My current method does not traverse to find if a node is a leaf node as I am not sure how to go about it, I have a basic check that looks like this:

    private static bool IsLeafNode(Node node)
    {
        int TotalLeafs(Node node)
        {
            int j = 0;
            for (int i = 0; i < node.Nodes.Count; i++){
                Node n = node.Nodes[i];
                j += n.Nodes.Count == 1 ? 1 : 0; //if leaf add 1
            }
            return j;
        }

//has 1 connection OR all its connections lead to nodes that have 1 connection
        return node.ConnectionCount == 1 || TotalLeafs(node) == node.Nodes.Count;
    }

The problem here is it does not consider the two leaf nodes that have 2 connections (but it is obvious still that they are leaf nodes).

How might I go about eliminating all the nodes that are leaf nodes?

The only way that I can see this being done is to traverse the node connections recursively and finding out if the node can be traversed back onto itself without visiting a node it has already visited. If it can't accomplish this, it must be a leaf node. — Hayden, Apr 14 '22 at 03:57
Do you have access to all the nodes in your graph? Can you create a copy of your graph and work (and change) with the copy instead? Do you want to check only one specific node or do you want to get all leaf nodes anyway? — Progman, Apr 15 '22 at 10:19
@Progman i have access to them all as all the nodes as a list of nodes and each node connects a list of who they connect to — WDUK, Apr 16 '22 at 00:37
Does this answer your question? [Finding all cycles in undirected graphs](https://stackoverflow.com/questions/12367801/finding-all-cycles-in-undirected-graphs) — Progman, Apr 16 '22 at 07:12
No i am not looking for cycles, i am looking to remove leaves `before` i search for cycles so I have less nodes to search through. — WDUK, Apr 16 '22 at 08:12

score 1 · Answer 1 · answered Apr 15 '22 at 08:11

at the note from Hayden, the nature of this problem is recursive, what a useless statement but .. still bare with me...

Consider the following picture, and let me you submit this initial proposal,

to decide if yes or no, a node (1) is a leaf (as you defined), I will execute a Depth first traverse from each of its children (2), (5), ignoring the edges to (1), and the DFS will simply return all the found nodes, if these lists do not contain edge 1, i can state there is no other path that from 1 leads back to 1 and thereforee no cycle.

Once we agree on this, then maybe there is maybe an even more powerful proposal... When executing a DFS traversal from everywhere, the stack of nodes defines a current path thru these nodes, ... therefore at anytime we travel to a node which is already on that stack, we found a cycle -> And all of these nodes are part of cycle and therefore must be excluded to the "leaves"

Well your suggestion seems to be that finding the cycles, means we also find the leaves. But the idea was to find the leaves, strip them, THEN find the cycles so there was less nodes to search through. A sort've pre-optimisation. But it doesn't sound like it will really give me much optimisation overall. — WDUK, Apr 16 '22 at 08:14

score 0 · Accepted Answer · answered Apr 16 '22 at 15:29

You can do a backwards search by starting at the known leaves, and recursively checking their neighbor if they are leaves as well. But each time when you check the number of connections, you have to "remove" the nodes which you have already considered to be leaves. If the resulting number of connection is zero or one, you found a leaf. The algorithm can look like this:

Create a new empty Set of leaves named foundLeaves.
Find all the "real" leaves in your graph, which have only one connection. Put them in a Set of nodes named leavesToCheck.
While the leavesToCheck set is not empty:
- Pick and remove one node from leavesToCheck.
- Check the number of connections this node have, minus the nodes which are already in the foundLeaves set:
  - When the number of connections is zero or one: You found a leaf. Add the found leaf into foundLeaves and add the neighbor of that node (if there is one) to the leavesToCheck set to check in the future.
  - When the number of connections is greater or equal two: Do nothing.

Eventually, the leavesToCheck set becomes empty. At that point the foundLeaves set contains all the nodes, which are considered leaves by your definition and have no cycles.

Of course, you can use other data structures like lists or queues for the foundLeaves and leavesToCheck collections. If your overall goal/algorithm supports it that you can remove the leaf nodes from the graph, you can do that. That way you don't need the foundLeaves list.

heothesennoc · Answer 3 · 2023-02-15T19:59:28.647

A bridge of a graph is an edge whose removal increases the number of components of the graph. So by definition, an edge which is a bridge cannot be part of a cycle.

In order to find your target nodes, you can:

Remove all the bridges. This will remove all the edges that are not part of a cycle. One of the famous algorithms to find bridges is Tarjan's algorithm.
Find the nodes that do not have any attached edges. Those are the nodes that are not part of any cycle.

Find all nodes that are a leaf in a graph

3 Answers3