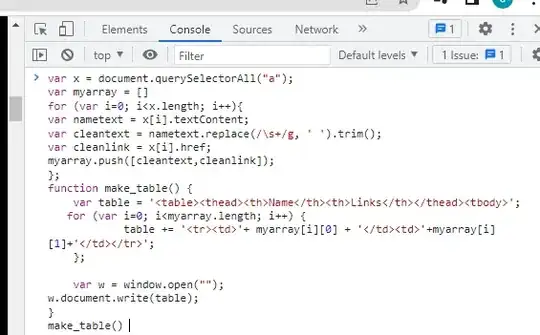
I am trying to solve an optimal control problem that involves minimizing an integral objective with fixed states but free terminal time. It is a relatively simple problem that can be solved analytically. Gekko's solution doesn't match the analytical. If I relax the lower bound of terminal time, then I am getting something close to the analytical solution. Am I doing anything wrong in the Gekko code?
I had earlier posted a similar question here.
The analytical solution is given as follows. (lambda is the Lagrange multiplier)
from gekko import GEKKO
import numpy as np
import matplotlib.pyplot as plt
# constants
k1 = 0.5
k2 = 0.1
k3 = 0.5
g = 0.5
# create GEKKO model
m = GEKKO()
# time points
n = 501
# tm = np.array([0,1e-5,1e-4,1e-2])
# tm = np.hstack((tm,np.linspace(1e-1, 1, n)))
tm = np.linspace(0, 1, n)
m.time = tm
# Variables
x1 = m.Var(value=1,lb=0,ub=1) # x1
u = m.MV(value=0.1,fixed_initial=False,lb=0,ub=1)
u.STATUS = 1
u.DCOST = 1e-5
J = m.Var(value=0.0) # objective function differential form intial value
p = np.zeros(len(tm))
p[-1] = 1.0
final = m.Param(value=p)
# FV
tf = m.FV(value=0.1, lb=3, ub=5.0)
tf.STATUS = 1
# equations
m.Equation(x1.dt()/tf == -u -g*x1)
m.Equation(J.dt()/tf==k1*k3*(u-k2)/(u+k3))
# Final conditions
soft = True
if soft:
# soft terminal constraint
m.Minimize(final*1e5*(x1-0)**2)
m.Minimize(final*1e5*(u-0)**2)
# m.Minimize(final*1e5*(x2-2)**2)
else:
# hard terminal constraint
x1f = m.Param()
m.free(x1f)
m.fix_final(x1f, 0)
uf = m.Param()
m.free(uf)
m.fix_final(uf, 0)
# connect endpoint parameters to x1 and x2
m.Equations([x1f == x1])
m.Equations([uf == u])
# Objective Function
# obj = m.Intermediate(m.integral((u-k2)/(u+k3)))
obj = m.Intermediate(J)
m.Maximize(obj*final)
m.options.IMODE = 6
m.options.NODES = 3
m.options.SOLVER = 3
m.options.MAX_ITER = 50000
# m.options.MV_TYPE = 0
# m.options.DIAGLEVEL = 0
m.solve(disp=True)
plt.close('all')
tm = tm * tf.value[0]
# Create a figure
plt.figure(figsize=(10, 4))
plt.subplot(2, 2, 1)
# plt.plot([0,1],[1/9,1/9],'k2:',label=r'$x<\frac{1}{9}$')
plt.plot(tm, x1.value, 'k-', lw=2, label=r'$x1$')
plt.ylabel('x1')
plt.legend(loc='best')
plt.subplot(2, 2, 2)
plt.plot(tm, u.value, 'k2--', lw=2, label=r'$u$')
plt.ylabel('control')
plt.legend(loc='best')
plt.xlabel('Time')
plt.subplot(2, 2, 3)
plt.plot(tm, J.value, 'g-', lw=2)
plt.text(0.5, 3.0, 'Final Value = '+str(np.round(obj.value[-1], 2)))
plt.ylabel('Objective')
plt.legend(loc='best')
plt.xlabel('Time')
plt.subplot(2, 2, 4)
U = np.array(u.value)
G =k1*k3*(U-k2)/(U+k3)
plt.plot(tm, G, 'g-', lw=2)
plt.text(0.5, 3.0, 'Final Value = '+str(np.round(obj.value[-1], 2)))
plt.ylabel('Gopt')
plt.legend(loc='best')
plt.xlabel('Time')
plt.show()