Selecting peak areas from 2D matrices

Question

Suppose we have an array like this :

A = peaks
A(A<0)=0   % Remove negative values to make things a bit more simple.

I would like to write a script that is able to select the whole volume of the peaks contained in A.

For example, include all the values that surround a local maximum, until it hits values which are either 0 or a local minimum.

Below is a link to an answered question on a similar but more complicated topic.
Find peak (regions) in 2D data

I tried to use the method found on the answer to the question above, but I had little success for my example. I understand that in this answer, on the line:

im3=imextendedmax(im2,10);

, the value 10 acts as some kind of threshold. If I leave the threshold value at 10, it only selects the upper part of the highest of the three peaks (kind of like selecting the snowy top of a mountain, but I would like the whole mountain). I tried to lower it in order to select the entirety of the peaks, but this is the result I get:

In these results, 6 peaks are identified, but what I want is 3 separated peaks, as described in the picture below:

Hope this is clear enough.

Answer 1

There might be better (faster) approaches, but the following one seems to be working fine.

So the problem with what you want to do is that although it is possible to find the positions of the local maximas like in the SO post you mention, the image must go through several transforms, which makes it impossible to get back the whole connected regions afterwards.

Let's quickly look at the code from the SO post, adapted to your problem:

% Image
im = peaks(150);
im(im<0)=0;

 % tophat transform
im2=imtophat(im,strel('disk',5));

% extended maximums
im3=imextendedmax(im2,10);

% Extract each blob
s=regionprops(im3,'Centroid','PixelIdxList');

figure,imagesc(im),axis image

for i=1:numel(s)
    x=ceil(s(i).Centroid);
    tmp=im*0;
    tmp(s(i).PixelIdxList)=1;
    tmp2=tmp.*im2;

% The maximum amplitude and location

    [refV,b]=max(tmp2(:));
    [x2,y2]=ind2sub(size(im),b);

% select the region around local max amplitude    
    tmp=bwselect(im2>refV*0.6,y2,x2,4);  

    [xi,yi]=find(tmp);
    hold on, plot(yi,xi,'r.')
    hold on, text(y2+10,x2,num2str(i),'Color','white','FontSize',16)    
end

Now there is still a set of parameters that you can act on: tmp=bwselect(im2>refV*0.6,y2,x2,4);

This selects from the imtophat transformed image, the patch of elements that are close from the point (x2,y2), and for which the values are >refV*0.6, where refV is the value at the local maxima. By playing on the coefficient 0.6, and applying bwselect to your initial image im, it is possible to achieve what you want, using an optimization algorithm:

The optimization problem

What we want here, is to select the maximum amount of pixels that are linked to each local maximum, in the sense of "All the points that are returned by the call to bwselect for a given local maxima, but are not belonging to another maxima"

The scoring function

Like with all optimization algorithm we are gonna need a function that give a score to a set of Tresholds to be fed to the bwselect function tmp=bwselect(im2>refV*T(i),y2,x2,4);

My choice for this scoring function is as follows :

To exclude overlapping solutions (i.e. points belonging to several peaks at the same time), these will be scored +Infty (or 1e6 in my example)

For the others, we will count the number of pixels that don't belong to any patch. The optimal solution will be the solution where the peaks don't overlap but that cover the maximum amount of pixels, i.e the solution with the smallest score.

The code for the scoring function:

function score = Get_patches(s,im,T)

xi = cell(numel(s),1);
yi = cell(numel(s),1);

score = numel(im);

Left_Mtrx = ones(size(im));

for i=1:numel(s)

    tmp=im*0;
    tmp(s(i).PixelIdxList)=1;
    tmp2=tmp.*im;
    
    % The maximum amplitude and location
    
    [refV,b]=max(tmp2(:));
    [x2,y2]=ind2sub(size(im),b);
    
    % select the region around local max amplitude
    tmp=bwselect(im>refV*T(i),y2,x2,4);
    
    [xi{i},yi{i}]=find(tmp);
    bi = find(tmp);
    
    b_taken = find(~Left_Mtrx);
    
    if ~isempty(intersect(b_taken,bi))
        
        score = 1e6;
        break;
    
    else
        
        score = score - numel(bi);
        Left_Mtrx(bi) = 0;
        
    end

end

end

The optimization

Now, what we need to do is to apply the particle swarm algorithm to your problem, using the previously mentioned scoring function:

% Image
im = peaks(150);
im(im<0)=0;

% tophat transform
im2=imtophat(im,strel('disk',5));

% extended maximums
im3=imextendedmax(im2,0.2);

% Extract each blob
s=regionprops(im3,'Centroid','PixelIdxList');

figure,imagesc(im),axis image

fun = @(T) Get_patches(s,im,T);

% Particle swarm optimization
% Initial positions of particles and best positions of particle
Pop_Size = 100;
Pos = rand(numel(s),Pop_Size);
Best_Pos = Pos;

% Get the best particule in the swarm
Best_Score = 1e6;
g = ones(3,1);

for jj=2:Pop_Size
    
    score = fun(Pos(:,jj));
    
    if score < Best_Score
        
       g = Pos(:,jj); 
       
       Best_Score = score;
       
    end
    
end

% Initialize particles speed
V = -1 + 2*rand(numel(s),Pop_Size);

% Number of iterations of the swarm
Nite = 100;
Count = 0;

% Particle swarm optimization parameters
w = 0.5;
Phi_p = 1;
Phi_g = 1;

% Initialize the scores
scores = zeros(1,Pop_Size);

while Count < Nite
    
    Count = Count +1;
    
    for ii = 1:Pop_Size
                    
        Rp = rand(numel(s),1); Rg = rand(numel(s),1);
        
        V(:,ii) = w*V(:,ii) + Phi_p*Rp.*(Best_Pos(:,ii)-Pos(:,ii)) + Phi_g*Rg.*(g-Pos(:,ii));
        
        Pos(:,ii) = Pos(:,ii) + V(:,ii);

        scores(ii) = fun(Pos(:,ii));
        
        if any(Pos(:,ii)<0) || any(Pos(:,ii)>1)
            
           scores(ii) = 1e6; 
            
        end
        
        BP_score = fun(Best_Pos(:,ii));
        
        if scores(ii) < BP_score
            
            Best_Pos(:,ii) = Pos(:,ii);
            
            if scores(ii) < Best_Score
                
               g =  Pos(:,ii);
               
               Best_Score = scores(ii);
                
            end
            
        end

    end

end


% Get better (minimum) score
idx_Best = find(scores == min(scores));

Best_tresholds =  Pos(:,idx_Best(1));

for i=1:numel(s)
    
    tmp=im*0;
    tmp(s(i).PixelIdxList)=1;
    tmp2=tmp.*im;
    
    % The maximum amplitude and location
    
    [refV,b]=max(tmp2(:));
    [x2,y2]=ind2sub(size(im),b);
    
    % select the region around local max amplitude
    tmp=bwselect(im>refV*Best_tresholds(i),y2,x2,4);
    
    [xi,yi]=find(tmp);
    
    hold on, plot(yi,xi,'r.')
    hold on, text(y2+10,x2,num2str(i),'Color','white','FontSize',16)
    
    
end

Output

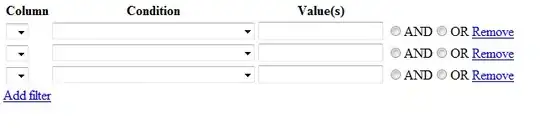
If you want to extract the values in your original array corresponding to each region:

[sz1,sz2] = size(im);
Output_Matrices = zeros(sz1,sz2,numel(s));

for i=1:numel(s)
    
    tmp=im*0;
    tmp(s(i).PixelIdxList)=1;
    tmp2=tmp.*im;
    
    % The maximum amplitude and location
    
    [refV,b]=max(tmp2(:));
    [x2,y2]=ind2sub(size(im),b);
    
    % select the region around local max amplitude
    tmp=bwselect(im>refV*Best_tresholds(i),y2,x2,4);
    
    [xi,yi]=find(tmp);
    
    hold on, plot(yi,xi,'r.')
    hold on, text(y2+10,x2,num2str(i),'Color','white','FontSize',16)
    
    % Your output matrix i-th slice holds the values for the i_th peak
    Output_Matrices(xi,yi,i) = im(xi,yi); 


end

Answer 2

I am posting another separate answer to this question because it is a completely different approach, and it is complementary to the first one depending on the specific problem you are trying to solve

This approach is based on another definition of "Being inside a peak".

We will say that a point (Xi,Yi) belongs to the peak #k if, when doing a gradient ascent, the position (Xi_,Yi_) (Iterating during the ascent), converges to the position of the maximum of the peak #k.

This process can be visualized by using quiver:

[X,Y]=meshgrid(1:150,1:150);
[px,py]=gradient(im);
figure;quiver(X,Y,px,py,2.5);

We will use the approach presented here to get the indexes of the maximas:

% Image
Npts = 150;
im = peaks(Npts);
im(im<0)=0;

 % tophat transform
im2=imtophat(im,strel('disk',5));

% extended maximums
im3=imextendedmax(im2,0.2);

% Extract each blob
s=regionprops(im3,'Centroid','PixelIdxList');

xmaxes = zeros(numel(s),1);
ymaxes = zeros(numel(s),1);

for ii=1:numel(s)
    x=ceil(s(ii).Centroid);
    tmp=im*0;
    tmp(s(ii).PixelIdxList)=1;
    tmp2=tmp.*im2;

% The maximum amplitude and location

    [refV,b]=max(tmp2(:));
    [ymaxes(ii),xmaxes(ii)]=ind2sub(size(im),b);

end

And then do the gradient ascent:

% 2D gradient matrices
[px,py]=gradient(im);
Norm_p = sqrt(px.^2+py.^2);
px(Norm_p>0) = px(Norm_p>0)./Norm_p(Norm_p>0); % Normalized
py(Norm_p>0) = py(Norm_p>0)./Norm_p(Norm_p>0);

px_ = px; % Temp var to be modified during the loop
py_ = py; 

idx = find(im > 0);

[X,Y] = meshgrid(1:Npts,1:Npts);
X_ = X;
Y_ = Y;

% Out of loop measure
eps = 1;

while eps > 1e-6

    % Follow the local normalized gradient direction
    X_(idx) = X_(idx) + px_(idx);
    Y_(idx) = Y_(idx) + py_(idx);
    
    % Clip back in the points that escape the grid
    X_(X_>Npts) = Npts;
    X_(X_<1) = 1;
    Y_(Y_>Npts) = Npts;
    Y_(Y_<1) = 1;
    
    % Interpolate gradient on the new positions
    px_(idx) = interp2(X,Y,px,X_(idx),Y_(idx));
    py_(idx) = interp2(X,Y,py,X_(idx),Y_(idx));
    
    
    % Out of loop cirterion, gets smaller as we reach maximas
    eps = max(sqrt(px_(idx).^2+py_(idx).^2));

end

Now we build a filter matrix, linking each point to the maximum it converged to:

% Build filter matrix
filtMtx = zeros(size(im));

for ii=1:numel(s)

    % Get all points that converged to the current max
    Dist2max = 100*ones(size(im)); % Initialize to high distance
    Dist2max(idx) = sqrt((X_(idx)-xmaxes(ii)).^2+(Y_(idx)-ymaxes(ii)).^2);
    
    filtMtx(Dist2max<1) = ii;
    
end

Finally, we can visualize the data:

% Output
figure,imagesc(im),axis image

ColSpcs = {'.r','.g','.b','.c','.m','.y','.k','.w'};

for ii=1:numel(s)
    
    hold on, plot(X(filtMtx == ii),Y(filtMtx == ii),ColSpcs{ii});
    hold on, text(xmaxes(ii)+10,ymaxes(ii),num2str(ii),'Color','white','FontSize',16);
    
end

Note that the matrix filtMtx allows you to index each peak, X(filtMtx == ii),Y(filtMtx == ii),im(filtMtx == ii) are the (X,Y,Z) coordinates of all the points related to peak ii.

Please also note that this way doesn't guarantee you that all points will be linked to a maxima (for example, local minima have nil gradient and will not be linked to anything), but it guarantees that most of your points will.